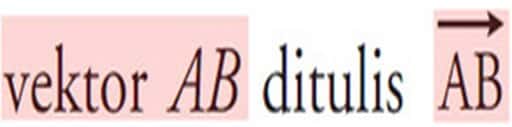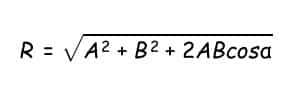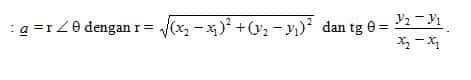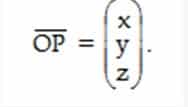Baca Cepat tampilkan
Memasuki abad 20, perkembangan Ilmu Pengetahuan dan Teknologi sangatlah pesat. Berbagai piranti sederhana maupun elektronik telah berhasil dibuatuntuk memudahkan pekerjaan manusia. Keberhasilan demi keberhasilan yang diraih manusia, tidak lepas atau bahkan sangat bergantung dari keberadaan suatu ilmu, yakni ilmu Fisika.
Fisika memiliki kaitan erat dengan matematika. Hal ini karena matematika mampu menyediakan kerangka logika di mana hukum-hukum fisika dapat diformulasikan secara tepat. Definisi, teori, dan model fisika selalu dinyatakan menggunakan hubungan matematis.
Sebagai ilmu dasar, fisika memiliki pengaruh pada banyak ilmu sains lainnya. Salah satu contohnya pada ilmu kimia. Fisika banyak mempelajari partikel renik semacam elektron. Bahasan tersebut ternyata juga dipelajari dan dimanfaatkan pada ilmu kimia. Bahkan topik mekanika kuantum yang diterapkan pada ilmu kimia telah melahirkan bidang baru yang dinamakan kimia kuantum (quantum chemistry).
Selain itu, ilmu fisika yang diterapkan pada bidang ilmu lain ikut berperan dalam melahirkan bidang studi baru yang menarik. Di antaranya adalah biofisika (fisika pada ilmu biologi), geofisika (fisika pada ilmu bumi), fisika medis (fisika pada ilmu kedokteran), dan yang lebih baru adalah ekonofisika (fisika pada ilmu ekonomi).
Fisika adalah ilmu yang mempelajari keteraturan alam semesta dan sebisa mungkin memanfaatkan keteraturan ini untuk dua hal, yaitu menemukan keteraturan lainnya di alam semesta yang belum ditemukan dan memanfaatkan keteraturan yang telah ditemukan untuk menjadi bermanfaat bagi kehidupan manusia.
Tanpa ada penemuan tentang keteraturan lensa, maka tidak mungkin di temukan planet-planet, tanpa ditemukannya planet-planet, tidak mungkin ditemukan Hukum-hukum Kepler, tanpa ditemukan Hukum Kepler, maka tidak mungkin ditemukan hal-hal penting lainnya di tata surya, dan hal-hal ini masih terus berlanjut, keteraturan yang telah ditemukan akan menjadi dasar untuk menemukan keteraturan-keteraturan lainnya.
Dengan demikian, Vektor merupakan pengetahuan yang sangat penting. Hal itulah yang melatar belakangi kami untuk menyusun makalah ini, agar nantinya dapat memahami dan mengaplikasikannya di kehidupan sehari-hari.
Pengertian Vektor
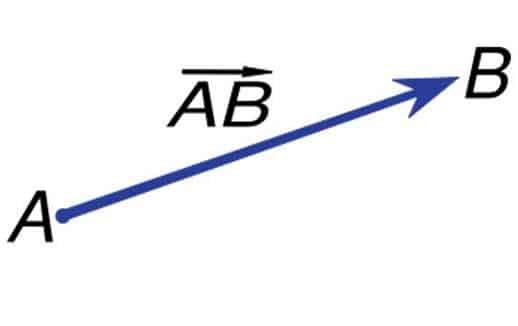
Secara sederhana pengertian vektor adalah besaran yang mempunyai nilai dan arah. Contoh dari besaran ini misalnya perpindahan, kecepatan, percepatan, gaya, dan sebagainya. Untuk menggambarkan vektor digunakan garis berarah yang bertitik pangkal. Panjang garis sebagai nilai vektor dah anak panah menunjukkan arahnya. Simbol vektor menggunakan huruf kapital yang dicetak tebal (bold) atau miring dengan tanda panah di atasnya seperti gambar berikut:
Menggambar sebuah Vektor
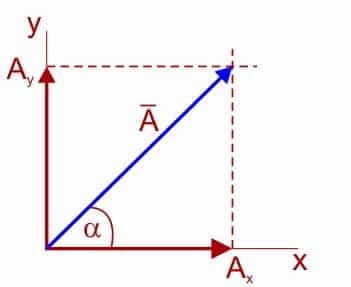
Vektor pada bidang datar mempunyai 2 komponen yaitu pada sumbu x dan sumbu y. Khusus untuk vektor yang segaris dengan sumbu x atau y berarti hanya mempunyai 1 komponen. Komponen vektor adalah vektor yang bekerja menuyusun suatu vektor hasil (resultan vektor). Oleh karenanya vektor bisa dipindahkan titik pangkalnya asalkan tidak berubah besar dan arahnya.
Secara matematis vektor dapat dituliskan A = Ax+Ay dimana A adalah resultan dari komponen-komponenya berupa Ax dan Ay.
Baca Juga: Angka Romawi
Sifat-Sifat Vektor
-
Komutatif
a + b = b + a
- Assosiatif
a + ( b + c) = (a + b) + c
- Memiliki elemen satuan atau elemen identitas
a + 0 = 0 + a = a
- Memiliki elemen inverse
a + (-a) = (-a) + a = 0
- Distributive dengan perkalian skalar
K(a + b) = ka + kb , dengan k= skalar
Penjumlahan Vektor
Inti dari operasi penjumlahan vektor ialah mencari sebuah vektor yang komponen-komponennya adalah jumlah dari kedua komponen-komponen vektor pembentuknya atau secara sederhana berarti mencari resultan dari 2 vektor. Aga susah memang dipahami dari definisi tertulis. Kita coba memahaminya dengan contoh.
Untuk vektor segaris, resultannya
R = A + B + C + n dst…
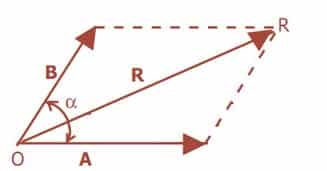
untuk penjumlahan vektor yang tidak segaris misalnya seperti gambar di bawah ini
rumus penjumlahan vektor bisa didapat dari persamaan berikut.
Baca Juga:Rumus Phytagoras
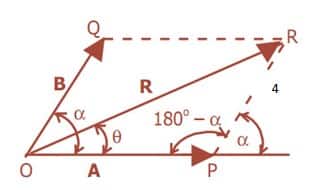
Menurut aturan cosinus dalam segitiga,
(OR)2 = (OP)2 + (PR)2 – 2(OP)(PR) cos (180o – α)
(OR)2 = (OP)2 + (PR)2 – 2(OP)(PR) cos (-cos α)
(OR)2 = (OP)2 + (PR)2 – 2(OP)(PR) cos α
Jika OP = A, PR = B, dan Resultan ‘R’ = ORmaka didapat persamaan
R2 = A2 + B2 – 2AB cos α
Rumus menghitung resultan vektornya
Dalam penjumlahan vektor sobat hitung bisa menggunakan 2 cara
- Penjumlahan Vektor dengan cara Jajar Genjang (Pararelogram)
yaitu seprti yang dijelaskan di atas. Metode yang digunakan adalah dengan mencari diagonal jajar genjang yang terbentuk dari 2 vektor dan tidak ada pemindahan titik tangkap vektor.
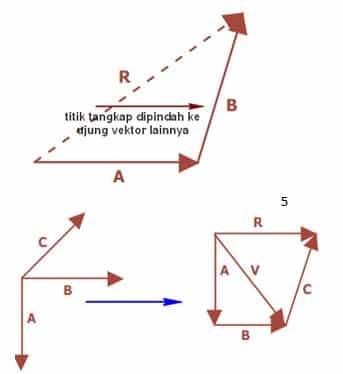
- Penjumlahan Vektor dengan Cara Segitiga
Pada metode ini dilakukan pemindahan titik tangka vektor 1 ke ujung vektor yang lain kemudian menghubungkan titi tangkap atau titik pangkal vektor pertama dengn titik ujung vektor ke dua. Lihat ilustrasi gambar di bawah ini.
Untuk vektor yang lebih dari 2, sama saja. Lakukan satu demi satu hingga ketemu resultan akhirnya. Dari gambar di atas, V = A + B dan R = V + C atau R = A + B + C.
Baca Juga:Rumus Standar Deviasi
Pengurangan Vektor
Pengurangan Vektor pada prinsipnya sama dengan penjumlahan, cuma yang membedakan adalah ada salah satu vektor yang mempunyai arah yang berlawanan. Misalnya vektor A bergerak ke arah timur dan B bergerak ke arah barat maka resultannya.
R = A + (-B) = A – B
Rumus Cepat Vektor
Berikut rumus cepat panduan mengerjakan soal vektor fisika :
Jika α = 0o maka R = V1 + V2
Jika α = 90o maka R = √(V12 + V22)
Jika α = 180o maka R = | V1 + V2 | –> nilai mutlak
Jika α = 120o dan V1 = V2 = V maka R = V
Contoh Soal
Dua buah vektor sebidang erturut-turut besarnya 8 satuan dan 6 satuan, bertitik tangkap sama dan mengapit sudut 30o Tentukan besar dan arah resultan vektor tersebut tersebut!
Jawaban :
R = 82 + 62 + 2.6.8.cos 30
R = 64 + 36 + 96 0,5 √3
R = 100 + 48√3
Baca Juga:Rumus Luas Segitiga
Perkalian Vektor dengan Skalar
Perkalian antara vektor dan skalar adalah hasil kali suatu skalar k dengan sebuah vektor A, sehingga dapat dituliskan kA dan didefinisikan sebagai sebuah vektor baru yang besarnya adalah besar k dikalikan dengan besar A. Arah vektor yang baru ini sama dengan arah vektor A jika k positif dan berlawanan arah dengan vektor A jika k negatif.+
- Perkalian Titik (Dot Product)
Perkalian titik diantara dua vektor A dan B dapat ditulis A • B. Perkalian skalar dua vektor dapat dikitang sebagai perkalian antara besar salah satu vektor dengan komponen vektor lain dalam arah vektor yang pertama tadi. Maka pada perkalian vektor ini ada ketentuan, yaitu :
- Perkalian komponen vektor yang sejenis (searah) akan menghasilkan nilai 1, seperti : i • i = j • j = k • k = 1
- Perkalian komponen vektor yang tidak sejenis (saling tegak liris) akan menghasilkan nilai 0, seperti : i • j = j • k = k • i = 0
- Perkalian Silang (Cross Product)
Perkalian silang diantara dua vektor A dan B dapat ditulis A X B dan hasilnya adalah sebuah vektor lain C. Arah dari C sebagai hasil perkalian vektor A dan B didefinisikan tegak lurus pada bidang yang dibentuk oleh A dan B. Pada perkalian vektor ini ada ketentuan sebagai berikut :
i x i = 0 i x j = k j x i = -k
j x j = 0 j x k = i k x j = -i
k x k = 0 k x i = j i x k = -i
Baca Juga:Persamaan Nilai Mutlak
Vektor pada Bidang Datar R2 (Dimensi Dua)
Di dalam bidang datar (R2) suatu vektor yang titik pangkalnya di A (x1, y1) dan titik ujungnya di B (x2, y2) dapat dituliskan dalam bentuk komponen :
Dilukiskan sebagai :
Vektor dalam bidang datar juga dapat dinyatakan dalam bentuk :
- Kombinasi linear vektor satuan i, j , misalnya vektor = xi + yj.
- Koordinat kartesius, yaitu : = (a1, a2).
- Koordinat kutub, yaitu :
Baca Juga:Rumus Persamaan Kuadrat
Vektor Pada Ruang ( Dimensi 3)
Vektor di ruang 3 adalah vektor yang mempunyai 3 buah sumbu yaitu x , y , z yang saling tegak lurus dan perpotongan ketiga sumbu sebagai pangkal perhitungan.
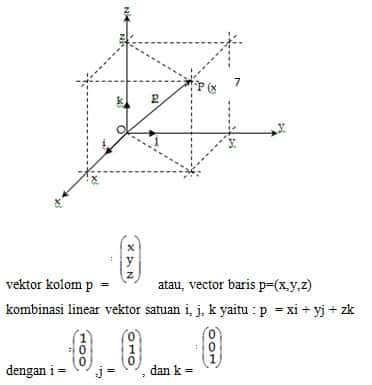
Vektor p pada bangun ruang dapat dituliskan dalam bentuk :
koordinat kartesius p = (x, y, z)
i = vektor satuan dalam arah OX
j = vektor satuan dalam arah OY
k = vektor satuan dalam arah OZ
Modulus Vektor
Modulus vektor yaitu besar atau panjang suatu vektor. Jika suatu vektor dengan koordinat titik A (x1 , y1 ,z1) dan B (x2 , y2 , z2) maka modulus (besar) atau panjang vektor dapat dinyatakan sebagai jarak antara titik A dan B yaitu :
Baca Juga:Logaritma Adalah
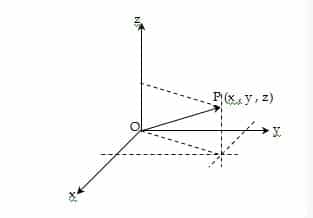
- Vektor Posisi
Vektor posisi titik P adalah vektor yaitu vektor yang berpangkal di titik O (0 , 0 , 0) dan berujung di titik P (x , y , z), bila ditulis.
Demikian penjelasan artikel diatas tentang Vektor Matematika – Pengertian, Oprasi, Rumus, Contoh, Perkalian semoga dapat bermanfaat bagi semua pembaca setia DosenPendidikan.Co.Id