Sin Cos Tan – Nilai, Cara Menghitung, Contoh Soal Dan Tabel – DosenPendidikan.Com– Fungsi trigonometri adalah fungsi dari sebuah sudut yang digunakan untuk menghubungkan antara sudut-sudut dalam suatu segitiga dengan sisi-sisi segitiga tersebut.
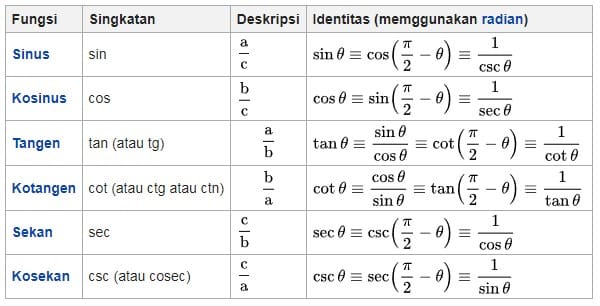
Fungsi trigonometrik diringkas di tabel di bawah ini. Sudut
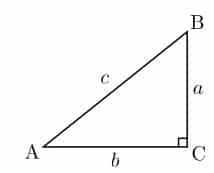
adalah sudut yang diapit oleh sisi miring dan sisi samping—sudut A pada gambar di samping, a adalah sisi depan, b adalah sisi samping, dan c adalah sisi miring:
Sin Cos Tan
Kali ini kita akan membahas pelajaran trigonometri lagi, buat adik-adik yang pernah membahas persoalan trigonometri semua pasti kenal dengan sudut-sudut istimewa. Bagi yang gak tau, mari kita ingat-ingat lagi
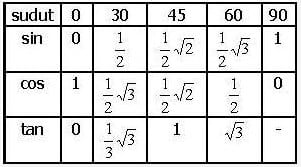
Sudut-sudut Istimewa Pada Kuadran I
Nah, untuk memahami dan menghafalkan sudut-sudut trigonometri, kita harus hafal dulu tabel sudut-sudut istimewa diatas. Kalo sudah, sekarang kita pahami konsep kuadran I, II, III dan IV
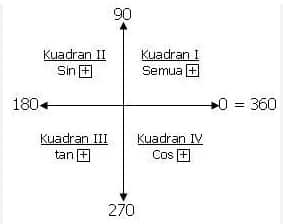
Memahami Konsep Kuadran
- Pada kuadran I (0 – 90) , semua nilai sin, tan dan cos bernilai positif —> “semua”
- Pada kuadran II (90 – 180) , hanya sin bernilai positif —> sin dibaca “sindikat”
- Pada kuadran II (180 – 270) , hanya tan bernilai positif —> tan dibaca “tangan”
- Pada kuadran II (270 – 360) , hanya cos bernilai positif —>cos dibaca “kosong”
Baca Juga : Rumus Deret Geometri
Jadi, untuk mengingat gambar diatas hafalkan kalimat : “Semua Sindikat Tangannya Kosong”
Mari sekarang, kita mempelajari tentang perubahan sudut.
Jika kita diminta untuk menghafalkan semua sudut-sudut trigonometri tentunya kesulitan karena tidak tahu konsepnya, seperti jika ditanya : berapa sin 330 ? Cos 315? tan 300 dan sebagainya. Pertanyaan tentang trigonometri sudut-sudut yang tidak ada pada tabel sudut istimewa tentunya membingungkan jika kita tidak tau cara praktisnya. Berikut akan saya bantu untuk memahaminya.
Misalkan kita mau menghitung sudut :
contoh 1 : Hitunglah nilai cos 210 ?
cos 210 —-> berada dikuadran III —-> pasti negatif, jadi jawaban harusnegatif
cos 210 = cos (180 +30) = – cos 30 = -1/2√3
jadi nilai cos 210 = – 1/2 √3 (minus setengah akar tiga)
contoh 2 : Hitunglah nilai sin 300 ?
sin 300 —-> berada di kuadran IV —-> pasti negatif, jadi jawaban harusnegatif
sin 300 = sin (270 + 30) = – cos 30 = 1/2√3
jadi nilai sin 300 = – 1/2 √3 (minus setengah akar tiga)
Nah, saya yakin masih ada yang bingung kan?? Kok bisa cos 210 = – cos 30, trus kok bisa sin 300 = – cos 30
Begini KONSEP nya : misalkan diketahui sudut sebesar x
JIka kita merubah sudut x menjadi sudut y maka kita dapat menggunakan patokan pada nilai 90, 180, 270, dan 360. Misalnya sudut 210 = sudut (180 + 30) atau boleh juga sudut 210 = sudut (270 – 60), yang penting di ingat, kita harus merubah sudut tersebut sehingga mengandung sudut-sudut istimewa pada kuadran satu seperti 30, 45, 60, sehingga mudah untuk menghitungnya.
Untuk Perubahan Sudut tadi ada hal yang terpenting untuk di pahami
JIka kita menggunakan 90 dan 270 maka konsepnya “BERUBAH”
sin berubah menjadi cos
cos berubah menjadi sin
tan berubah menjadi cotan
Jika kita menggunakan 180 dan 360 maka konsepnya “TETAP”
sin tetap menjadi sin
cos tetap menjadi cos
tan tetap menjadi tan
Mari untuk menutup pembahasan ini kita coba dengan contoh berikutnya,
contoh 3 : Hitung nilai sin 150 ?
sin 150 —-> berada dikuadran II —-> pasti positif, jadi jawaban haruspositif
sin 150 = sin (90 + 60) = + cos 60 = +1/2 (positif setengah) —–> ingat sudut 90 Konsep “Berubah”
atau
sin 150 = sin (180 – 30) = + sin 30 = +1/2 (positif setengah) —–> ingat sudut 180 KONSEP “TETAP”
Menghitung SIN COS TAN
Menghitung sin cos tan (fungsi trigonometri di Excel 2007). Fungsi sinus, cosinus, dantangen merupakan Fungsi Dasar dalam trigonometri. Excel menyediakan fungsi-fungsi trigonometri yang dapat digunakan dalam perhitungan nilai sinus ,cosinus, dantangen sebuah sudut.
Trigonometri adalah bagian dari matematika yang mempelajari relasi antara sudut dansisi-sisi pada suatu segitiga dan juga fungsi-fungsi dasar dari relasi-relasi tersebut. Trigonometri banyak digunakan di Bidang Sains dan teknik. Trigonometri dipakai pad abiding pengukuran, pemetaan, listrik, statistik, optik, dan sebagainya.
Fungsi-fungsi dalam excel antara lain sebagai berikut :
- Fungsi Finansial
- Fungsi Matematika dan Trigonometri
- Fungsi Statistika
- Fungsi Logika
Operator matematika yang akan sering digunakan dalam rumus adalah :
- + Penjumlahan
- – Pengurangan
- * Perkalian
- / Pembagian
- ^ Perpangkatan
- % Persentase
Proses perhitungan akan dilakukan sesuai dengan derajat urutan dari operator ini, dimulai dari pangkat (^), kali (*), atau bagi (/), tambah (+) atau kurang (-).
Baca Juga : Bilangan Prima Adalah
Fungsi Logika (Logical)
Fungsi ini digunakan dalam menentukan suatu tes secara logika yang dikerjakan dalam menampilkan hasil proses. Biasanya hasilnya berupa karakter yang bernilai True (benar yang bernilai 1) atau False (salah yang bernilai 0
- Fungsi Lookup dan Referensi (Lookup & Reference).
Digunakan untuk menampilkan informasi berdasar pada pembacaan dari suatu table atau criteria tertentu dalam daftar/tabel.
- Fungsi Tanggal dan Waktu (Date & Time).
Fungsi yang digunakan dalam melakukan perhitungan waktu berdasar detik, menit, jam, hari, bulan, dan tahun.
- Sinus
Rumus: =SIN(sudut dalam radian) atau =SIN(RADIANS (SUDUT))
Contoh: Carilah nilai sinus dari sudut 0º, 30º, 45º, 60º, dan 90º..!
Jawab:
Pada kolom Rumus, nilai A2, A3, dst diperoleh dengan cara meng-klik cell pada kolom Sudut (º)
- Cosinus
Rumus: =COS (sudut dalam radian) atau =COS(RADIANS(SUDUT))
Contoh: Carilah nilai sinus dari sudut 0º, 30º, 45º, 60º, dan 90º..!
Jawab:
Pada kolom Rumus, nilai A2, A3, dst diperoleh dengan cara meng-klik cell pada kolom Sudut (º)
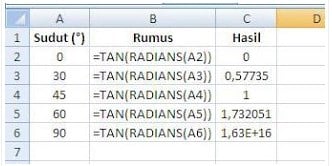
- Tangen
Rumus: =TAN(sudut dalam radian) atau =TAN (RADIANS(SUDUT))
Contoh: Carilah nilai sinus dari sudut 0º, 30º, 45º, 60º, dan 90º..!
Jawab:
Pada kolom Rumus, nilai A2, A3, dst diperoleh dengan cara meng-klik cell pada kolom Sudut (º)
Nilai TAN 90º adalah takter definisi
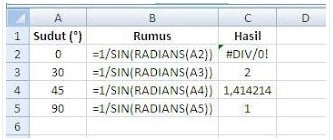
- Cosecan
Rumus: =1/SIN (sudutdalam radian) atau =1/SIN (RADIANS(SUDUT))
Contoh: Carilah nilai sinus dari sudut 0º, 30º, 45º, dan 90º..!
Jawab:
Baca Juga : Belah Ketupat
Pada kolom Rumus, nilai A2, A3, dst diperoleh dengan cara meng-klik cell padakolom Sudut (º)
Nilai COSEC 0º adalah takter definisi
- Secan
Rumus: =1/COS(sudut dalam radian) atau =1/COS (RADIANS(SUDUT))
Contoh: Carilah nilai sinus dari sudut 0º, 30º, 45º, dan 90º..!
Jawab:
Pada kolom Rumus, nilai A2, A3, dst diperoleh dengan cara meng-klik cell padakolom Sudut (º)
Nilai SEC 90º adalah takter definisi
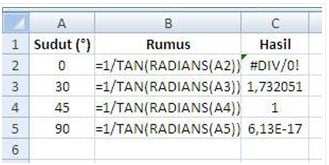
- Cotangen
Rumus: =1/TAN (sudutdalam radian) atau =1/TAN (RADIANS(SUDUT))
Contoh: Carilah nilai sinus dari sudut 0º, 30º, 45º, dan 90º..!
Jawab:
Padakolom Rumus, nilai A2, A3, dst diperoleh dengan cara meng-klik cell pada kolom Sudut (º)
Nilai COT 90º adalah takter definisi
Nilai Sin Cos Tan
Untuk mengingatnya orang biasanya memakai SINDEMI, KOSAMI dan TANDESA
sin theta = depan/miring (SINDEMI)
kos theta = samping/miring (KOSAMI)
tan theta = depan/samping (TANDESA)
Baca Juga : Keliling Lingkaran
Sin 0° = 0
Sin 30° = 1/2
Sin 45° = 1/2 √2
Sin 60° = 1/2 √3
Sin 90° = 1
Cos 0° = 1
Cos 30° = 1/2 √3
Cos 45° = 1/2 √2
Cos 60° = 1/2
Cos 90° = 0
Tan 0° = 0
Tan 30° = 1/3 √3
Tan 45° = 1
Tan 60° = √3
Tan 90° = ∞
Cosc A = 1/sin A
Sec A = 1/Cos A
Cotg A = 1/Tg A
Perhatikan skema berikut
Langkah – langkah:
- Menentukan kuadran sudut
- Mengubah sudut dalam bentuk yang bersesuaian.
- Kuadran II : 180 – a
- Kuadran III : 180 + a
- Kuadran IV : 360 – a
- Menentukan tanda (-/+) nilai sin cos dan tan.
Gunakan istilah“Semua Sudah Tau Caranya”.
Artinya, sesuai urutan kuadran, kuadran I( Semua positip), II( hanya Sin postip), III(hanya Tan positip), dan IV (hanya Cos positip)
Catatan: Semua langkah- langkah tersebut dirangkum dalam skema diatas. Contoh, akan ditentukan nilai Sin 150.
Baca Juga : Integral Trigonometri
- Menentukan kuadran sudut.
Sudut 150 berada di kuadran II
- Mengubah sudut dalam bentuk yang bersesuaian
Karena di kuadran II, sudut diubah dalam bentuk (180 – a), 150 = (180 – 30)
- Menentukan tanda -/+ Sin di kuadran II bertanda + Sin 150 = sin (180 –30)= + Sin 30 = 0,5
Jadi Sin 150 = 0,5
Lagi, akan ditentukan nilai Cos 210.
- Menentukan kuadran sudut.
Sudut 210 berada di kuadran III
- Mengubah sudut dalam bentuk yang bersesuaian.
Karena di kuadran III, sudut diubah dalam bentuk (180 + a), 210 = (180 + 30)
- Menentukan tanda -/+
Cos di kuadran III bertanda (-)