Siklus Carnot – Tahapan, Mekanisme, Daya Guna & Contoh Soal – Untuk pembahasan kali ini kami akan mengulas mengenai Siklus Carnot yang dimana dalam hal ini meliputi tahapan, mekanisme, daya guna dan contoh soal, nah agar dapat lebih memahami dan dimengerti simak ulasan selengkapnya dibawah ini.
Sebelum membahas siklus Carnot terlebih dahulu perlu diketahui istilah reversibel dan irreversibel. Sebuah proses reversibel didefinisikan sebagai sebuah proses yang dapat dibalik tanpa meninggalkan jejak pada lingkungan. Atau dengan kata lain, sebuah proses yang jika dibalik akan melalui lintasan yang sama-ingat pengertian panas dan kerja sebagai fungsi lintasan. Proses irreversibel adalah kebalikan dari proses reversibel.
Siklus Carnot
Siklus Carnot adalah sebuah siklus reversibel, yang pertama kali dikemukakan oleh Sadi Carnot pada tahun 1824, seorang insinyur Perancis. Mesin teoritis yang menggunakan siklus Carnot disebut dengan Mesin Kalor Carnot. Siklus Carnot yang dibalik dinamakan dengan siklus Carnot terbalik dan mesin yang menggunakan siklus carnot terbalik disebut dengan Mesin refrigerasi Carnot.
Baca Juga Artikel yang Mungkin Berkaitan : Kalorimeter
Siklus Carnot adalah proses termodinamik yang dialami oleh zat kerja (working substance) pada mesin Carnot. Siklus ini terdiri atas dua proses isotermal dan dua proses adiabatik. Pada proses isotermal pertama, yang terjadi pada temperatur lebih tinggi, zat mengalami ekspansi dan menyerap kalor.
Proses isotermal kedua, yang terjadi pada temperatur rendah, zat mengalami kompresi dan melepas kalor. Garis isotermal pertama dan kedua dihubungkan oleh dua proses adibatik. adiabatik pertama zat mengalami ekspansi, sedangkan adibatik kedua zat mengalami kompresi.
Tahapan Siklus Carnot
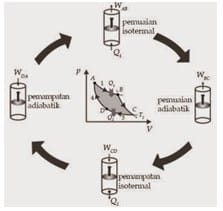
Siklus carnot terdiri dari 4 tahapan proses, sebagai berikut.
- Ekspansi isothermal reversible, dimana material ( working substance) menyerap kalor Q1 dari reservoir kalor pada temperature T1 dan sistem melakukan kerja.
- Ekspansi adiabatic reversible, dimana working substance berkurang temperaturnya dari T1 menjadi T2 dan sistem melakukan kerja.
- Kompresi isothermal reversible, dimana working substance melepaskan kalor Q2 ke reservoir dingin dengan tempertaur T2 dan kerja dikenakan terhadap sistem.
- Kompresi adiabatic reversible, dimana working substance dikembalikan ke keadaan awal (semula), temperature sistem berubah dari T2 menjadi T1 dan kerja dikenakan terhadap sistem.
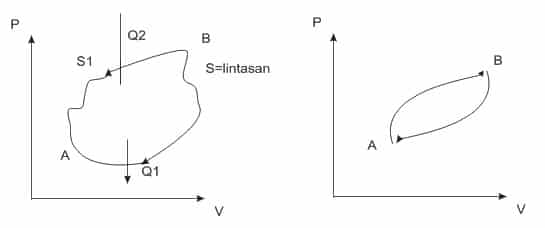
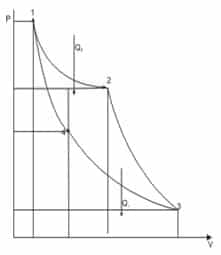
Keempat proses di atas dapat dilukiskan dalam bentuk diagram P versus V, seperti di bawah ini:
Mekanisme Kerja Siklus Carnot
Karena sistem dikembalikan ke keadaan semula, maka perubahan besaran keadaan (besaran termodinamika) seperti energi dalam maupun entalpi sistem proses adalah nol. Dengan menggunakan hukum I termodinamika dapat dihitung kalor dan kerja pada masing-masing tahap proses diatas.
Baca Juga Artikel yang Mungkin Berkaitan : Perpindahan Kalor
Misalnya substansi melakukan kerja adalah suatu gas ideal.
- Proses Ekspansi Isotermal Reversible
dU = đ Qrev – PdV atau dU = đ Qrev + dW
Proses Isotermal dU = 0, sehingga
đ W = đ Qrev = PdV
W1 = -Q1 = -nRT ln V2/V1
- Proses Ekspansi Adiabatik Reversibel
Pada proses adiabatic Q = 0, sehingga;
dU = đ W = -PdV
đ W = Cv(T2-T1), dimana T1>T2
Cv = kapasitas panas pada volume tetap
- Proses Kompresi Isotermal Reversibel
Dengan menggunakan penjelasan yang mirip dengan proses ekspansi isotermal reversibel, maka diperoleh kerja pada proses ini adalah:
W3 = -Q2 = -nRT ln V4/V3, dimana V3>V4
Baca Juga Artikel yang Mungkin Berkaitan : Hukum Hess adalah
- Proses Kompresi Adiabatik Reversibel
Dengan menggunakan penjelasan yang mirip dengan proses ekspansi adiabatik reversibel. Maka diperoleh kerja untuk proses ini adalah :
W4 = Cv (T1-T2), dimana T1>T2
Total kerja, W yang dilakukan oleh mesin carnot dalam satu siklus adalah
W = W1 + W2 + W3 + W4
W = -nRT ln V2/V1 + Cv (T2-T1) – nRT ln V4/V3 + Cv (T1-T2)
W = -nRT ln V2/V1 – nRT ln V4/V3
W = -Q1 – Q2
Q2 berharga negatif karena V4<V3. Sesuai dengan fakta bahwa kalor ini dilepaskan oleh sistem. Dengan demikian,
W = – Q1 + Q2 atau –W = Q1 – Q2
Kerja yang dilakukan oleh mesin adalah selisih antara kalor yang diserap, Q1 dengan kalor yang dilepaskan Q2.
Efisiensi mesin carnot, η adalah perbandingan antara kerja yang dilakukan mesin dengan kalor yang diserap, Q1.
η = -W/Q1
η = (Q1-Q2)/Q1 = 1-Q2/Q1
Sejumlah kalor Q1 diserap dari reservoir kalor yang temperaturenya T1, sejumlah kalor Q2 dilepaskan ke reservoir kalor yang temperaturnya T2 dan kerja dilakukan oleh sistem, demikian seterusnya. Kalor yang ditransfer tergantung pada beda temperatur antara dua reservoir tersebut. Temperatur reservoir ini disebut temperatur termodinamika T. karena Q2/Q1 sebanding dengan temperatur termodinamika dari reservoir, maka efisiensi mesin Carnot dapat dinyatakan sebagai berikut:
η = 1-T2/T1
Dari hasil yang diperolehnya, Carnot menyampaikan hasil teoremanya bahwa tidak ada mesin kalor yang bekerja antara dua reservoir kalor mempunyai efisiensi lebih besar dari mesin Carnot (ideal) yang bekerja pada dua reservoir kalor yang sama. Teorema diatas menunjukkan bahwa mesin kalor yang irreversibel mempunyai efisiensi lebih rendah dari mesin reversibel.
Baca Juga Artikel yang Mungkin Berkaitan : Reaksi Eksoterm adalah
Simpulan dari rumusan efisiensi mesin carnot:
- Semua mesin carnot yang bekerja pada dua reservoir kalor yang sama mempunyai efisiensi yang sama
- Efisiensi mesin kalor tidak tergantung pada jenis material (working substance) yang digunakan
- Temperatur termodinamika tidak tergantung pada jenis material (working substance)
Mesin Kalor Carnot
Ketika system dalam suatu mesin menjalani sebagian daurnya, sejumlah kalor diserap dari reservoir panas, pada bagian lain dari daur itu kalor yang jumlahnya lebih sedikit dibuang ke reservoir yang lebih dingin. Jadi boleh dikatakan bahwa mesin bekerja diantara sepasang reservoir ini. Menurut kenyataannya sejumlah kalor selalu dibuang ke reservoir yang lebih dingin, sehingga efisiensi mesin tidak akan pernah mencapai 100%.
Ada 3 hal yang penting mengenai mesin :
- Berapa daya guna maksimum yang dapat dicapai oleh suatu mesin yang bekerja antara kedua reservoir itu.
- Bagaimana karakteristik mesin.
- Apa pengaruh sifat zat kerja.
Untuk menjawab pertnyaan ini Nicelai Leonard Sadi Carnot (1824) seorang insinyur ulung bangsa Perancis memikirkan sebuah siklis ideal yang sekarang terkenal dengan siklus Carnot.
Suatu mesin yang menjalani siklus carnot disebut mesin carnot. Sedangkan mesin kalor carnot adalah suatu mesin yang mengubah energy kalor menjadi energy mekanik. Karena keempat proses dari siklus tersebut reversible maka siklus carnot adalah siklus reversible.
Q2= Kalor masuk
W= Usaha yang dihasilkan
Q1= Kalor yang keluar atau energy kalor yang tidak terpakai atau terbuang
Q2 dari reservoir panas, Q1 dari reservoir dingin.
Usaha W=Q2-Q1
Efisiensi mesin kalor :
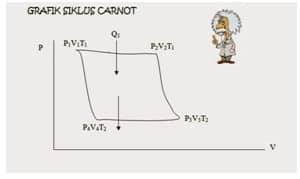
Grafik Mesin Kalor Carnot
Usaha 1-2 (Ekspansi isothermik)
Usaha 2-3 (Ekspansi adiabatic)
Usaha 3-4 (Kompresi isothermik)
Usaha 4-1 (Kompresi adiabatic)
Usaha total
Kita amati pada proses adiabatic
2 3
4 1
Efisiensi diatas merupakan Effisiensi Mesin Carnot Termik.
Effisiensi mesin secara umum dapat dituliskan sebagai:
η=Q2-Q1Q2
η=WQ2
Baca Juga Artikel yang Mungkin Berkaitan : Perubahan Fisika adalah
Dari persamaan diatas dapat disimpulkan bahwa:
Mesin biasa hanya berlaku persamaan
η=Q2-Q1Q1
Sedang mesin Carnot dapat berlaku
η=Q2-Q1Q1 dan η=T2-T1T2
Refrigerator Carnot (Mesin Pendingin Carnot)
Mengingat mesin Carnot merupakan mesin kalor reversible, maka mesin tersebut dapat dibalik. Mesin tersebut merupakan mesin pendingin atau refrigerator Carnot.
Pada refrigerator Carnot berlaku
T2′>T1, W=Q2-Q1
W= kalor yang masuk / diperlukan
Q1= kalor yang dihisap
Perbandingan antara kalor Q1 yang dapat dihisap dengan usaha yang digunakan W merupakan koefisien performance C.
c=T1’T2′-T1′
c=Q1’W’=Q1’Q2′-Q1′
Theorema Carnot berbunyi : “Tak ada sebuah mesin yang bekerja antara dua reservoir tertentu dapat lebih effisien daripada mesin Carnot yang bekerja antara kedua reservoir”.
Bukti:
Misalkan sebuah mesin Carnot (R) dan suatu mesin lain (I) bekerja diantara dua reservoir yang samadan diatur demikian sehingga keduanya melakukan usaha yang sama yaitu W.
Mesin Carnot R
- Menghisap kalor reservoir panas.
- Melakukan usaha W.
- Mengeluarkan kalor Q1-W kepada reservoir dingin
- Daya Guna ηR=WQ1
Mesin Lain I
- Menghisap kalor Q, dari reservoir panas.
- Melakukan usaha W
- Mengeluarkan kalor Q1′-W kepada reservoir dingin
- Daya guna η1=WQ’
Misalkan bahwa daya guna mesin I lebih besar dari R
ηI>ηR
WQ,>WQ1
Q1>Q’
Misalkan sekarang bahwa mesin I menjalankan mesin Carnot R yang bekerja sebagai mesin pendingin. Pada peristiwa ini secara simbolik ditunjukkan sebagai gambar:
Karena seluruh usaha adalah untuk kepentingan bersama maka mesin kalor dan mesin pendingin ini dapat digabungkan sehingga keseluruhannya merupakan alat yang bekerja sendiri.
Kalor bersih yang diserap dari reservoir dingin adalah:
Q1-W-Q1-W=Q1-Q1′
Harga ini adalah positif. Kalor bersih yang dikeluarkan kepada reservoir panas juga =Q1-Q1′
Jadi kesimpulannya alat yang bekerja sendiri ini memudahkan kalor sebesar Q1-Q1, dari reservoir dingin ke reservoir panas. Hal ini bertentangan dengan hukum II Termodinamika (Azas Clausius).
Hal ini berarti bahwa pengandaian ηI>ηR salah. Maka seharusnya adalah:
ηI≤ηR
Dari Theorema Carnot dapat ditarik kesimpulan bahwa:
Semua mesin Carnot yang bekerja antara dua reservoir yang tertentu daya gunanya sama.
Bukti:
Misalkan ada mesin Carnot R1 dan R2 yang bekerja diantara dua reservoir yang sama. Apabila R1 menjalankan R2 yang bekerja sebagai mesin pendingin maka theorema Carnot haruslah :
ηR1≤ηR2
Apabila R2 menjalankan R1 yang bekerja sebagai mesin pendingin maka menurut theorema Carnot haruslah:
ηR2≤ηR1
Jadi dengan begitu jelaslah bahwa
ηR1=ηR2
Karena dalam pembahasan tadi tidak terdapat syarat-syarat khusus untuk sifat zat kerja maka, daya guna siklus Carnot tidak dipengaruhi oleh zat kerja.
Daya Guna Siklus Carnot
Karena η Carnot tidak tergantung dari zat kerja maka untuk mudahnya perhitungan kita pakai gas sempurna sebagai gas kerja.
Skema suatu proses siklis
a → b Proses kompressi adiabatic reversible.
Persamaan : Vax-IT2=Vbx-IT1
Atau T1T2=VaVbx-I
b → c Proses ekspansi isothermik reversible.
Hukum I Thermodinamika :
dQ=dU+PdV
dQ=CVdT+P+∂U∂VTdV
Karena U gas ideal hanya merupakan fungsi dari suhu saja maka ∂U∂VT=0
Karena b→c merupakan proses isothermis maka CvdT=0
Jadi dQ=PdV=nRTVdV
Q1=VbVcnRT1dVV=nRT1lnVcVb
c → d Proses ekspansi adiabatic reversible
Persamaan : Vcx-IT1=Vdx-IT2
T1T2=VdVcx-I
Dari proses kompressi adiabatic reversible didapat bahwa :
T1T2=VaVbx-I
T1T2=VdVcx-I=VaVbx-I
d → a Proses kompressi isothermik reversible
Q2=VdVanRT2dVV=-nRT2VdVadVV=nRT2lnVaVd=nRT2lnVdVa
η=1-Q2Q1=1-nRT2lnVdVanRT1lnVcVb
VdVc=VaVb sehingga VdVa=VcVb
Η carnot=1-T2T1
Contoh Soal Siklus Carnot
Terdiri Atas:
1. Misalkan dalam iklan ditawarkan mesin yang bekerja dengan reservoir bersuhu 500 K dan 400 K memerlukan energy sebesar 4 x 104 joule dan melakukan usaha 107 joule. Berdasarkan hokum kedua Thermodinamika, dapatkah iklan itu dipercaya?
Penyelesaian:
η carnot = 1-Q2Q1=1-T2T1=1-400500=15×100%=20%
W = 104 Joule dan Q1 = 4. 104 joule
W = Q1-Q2
104=4. 104-Q2
Q2=4. 104-104=3. 104
η=1-3. 1044. 104=1-34100%=25%
η mesin > η carnot
Jadi iklan tidak dapat dipercaya.
2. Bagaimana halnya dengan iklan yang menawarkan mesin berefisiensi 30% bekerja dengan reservoir 400 K dan 900 K
Penyelesaian:
η carnot =1-Q2Q1=1-T2T1
=1-400.900100%=55%
η carnot=30%
η mesin < η carnot
Jadi iklan dapat dipercaya.
3. Buktikan bahwa kurva adiabatic gas ideal lebih tegak daripada kurva isotermik!
Penyelesaian:
Pada proses isotermik PV=C
Pada proses adiabatic PVγ=CI
P = CV = CV-I
dPdV=-CV-2=-CV2=-PV
P=C’VγC’V-γ
dPdV= -γC’V-γ-I= -γC’Vγ+1 = -γPV
Karena γ=CpCV selalu > 1 maka kurva adiabatic gas ideal lebih tegak dari pada kurva isotermik gas ideal.
Demikianlah pembahasan mengenai Siklus Carnot – Tahapan, Mekanisme, Daya Guna & Contoh Soal semoga dengan adanya ulasan tersebut dapat menambah wawasan dan pengetahuan anda semua, terima kasih banyak atas kunjungannya. 🙂 🙂 🙂