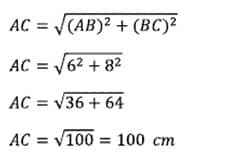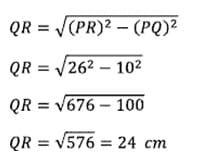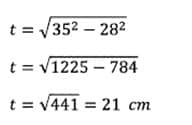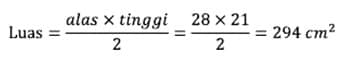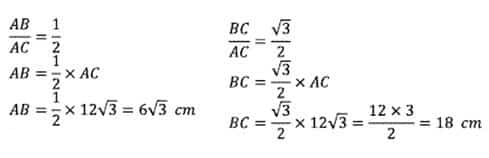Dalil PythagorasDalam ilmu Matematika, salah satu rumus yang paling di kenal dan sangat berguna adalah rumus Pythagoras. Rumus ini dinamai oleh Matematikawan Yunani yaitu Pythagoras (582 SM-496 SM). Walaupun fakta didalam rumus ini telah banyak diketahui sebelum lahirnya Pythagoras, namun rumus ini dipatenkan oleh Pythagoras karena beliau lah yang pertama membuktikan pengamatan ini secara matematis.
Ide dalam rumus Pythagoras ini adalah mengungkapkan panjang serta hubungan antara sisi-sisi pada suatu segitiga siku-siku. Dimana jika diketahui dua buah sisi (a) dan (b), maka kita dapat menemukan jarak terpendek antara kedua sisi dengan menghitung hipotenusa atau sisi miring (c) dari segitigsa siku-siku. Oleh krena itu, penggunaan rumus Phytagoras sangat penting bagi ilmu Matematika terutama pada Geometri. Rumus umum Pythagoras adalah: c2 = a2 + b2
Sejarah Teorema Pythagoras
Sejarah dari Teorema Pythagoras dapat dibagi sebagai berikut:
- pengetahuan dari Triple Pythagoras,
- hubungan antara sisi-sisi dari segitiga siku-siku dan sudut-sudut yang berdekatan, 3. bukti dari teorema.
Sekitar 4000 tahun yang lalu, orang Babilonia dan orang Cina telah menyadari fakta bahwa sebuah segitiga dengan panjang sisi 3, 4, dan 5 harus merupakan segitiga siku-siku. Mereka menggunakan konsep ini untuk membangun sudut siku-siku dan merancang segitiga siku-siku dengan membagi panjang tali ke dalam 12 bagian yang sama, seperti sisi pertama pada segitiga adalah 3, sisi kedua adalah 4, dan sisi ketiga adalah 5 satuan panjang.
Sekitar 2500 tahun SM, Monumen Megalithic di Mesir dan Eropa Utara terdapat susunan segitiga siku-siku dengan panjang sisi yang bulat. Bartel Leendert van der Waerden menghipotesis-kan bahwa Tripel Pythagoras diidentifikasi secara aljabar. Selama pemerintahan Hammurabi the Great (1790-1750 SM), tablet Plimpton Mesopotamian 32 terdiri dari banyak tulisan yang terkait dengan Tripel Pythagoras. Di India (Abad ke-8 sampai ke-2 sebelum masehi), terdapat Baudhayana Sulba Sutra yang terdiri dari daftar Tripel Pythagoras yaitu pernyataan dari dalil dan bukti geometris dari teorema untuk segitiga siku-siku sama kaki.
Pythagoras (569-475 SM) menggunakan metode aljabar untuk membangun Tripel Pythagoras. Menurut Sir Thomas L. Heath, tidak ada penentuan sebab dari teorema ini selama hampir lima abad setelah Pythagoras menuliskan teorema ini. Namun, penulis seperti Plutarch dan Cicero mengatributkan teorema ke Pythagoras sampai atribusi tersebut diterima dan dikenal secara luas. Pada 400 SM, Plato mendirikan sebuah metode untuk mencari Tripel Pythagoras yang baik dipadukan dengan aljabar and geometri.
Sekitar 300 SM, elemen Euclid (bukti aksiomatis yang tertua) menyajikan teorema tersebut. Teks Cina Chou Pei Suan Ching yang ditulis antara 500 SM sampai 200 sesudah masehi memiliki bukti visual dari Teorema Pythagoras atau disebut dengan “Gougu Theorem” (sebagaimana diketahui di Cina) untuk segitiga berukuran 3, 4, dan
Selama Dinasti Han (202 SM – 220 M), Tripel Pythagoras muncul di Sembilan Bab pada Seni Mathematika seiring dengan sebutan segitiga siku-siku. Rekaman pertama menggunakan teorema berada di Cina sebagai ‘theorem Gougu’, dan di India dinamakan “Bhaskara theorem”.
Namun, hal ini belum dikonfirmasi apakah Pythagoras adalah orang pertama yang menemukan hubungan antara sisi dari segitiga siku-siku, karena tidak ada teks yang ditulis olehnya yang ditemukan. Walaupun demikian, nama Pythagoras telah dipercaya untuk menjadi nama yang sesuai untuk teorema ini.
Dalil Pythagoras
Dalil Pythagoras mengungkapkan hubungan antara sisi-sisi pada suatu segitiga siku-siku. Banyak permasalahan sehari-hari yang berkaitan dengan segitiga siku-siku atau sudut siku-siku, misalnya:
- Menentukan sisi miring dari sisi miring suatu kuda-kuda rumah.
- Membuat pojok-pojok suatu lapangan bola volly agar betul-betul siku-siku.
Melalui penerapan dalil Pythagoras permasalahan itu akan dapat diselesaikan
Bunyi Teorema Pythagoras
Teorema Pythagoras berbunyi:
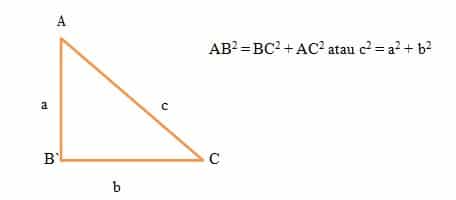
pada suatu segitiga siku-siku berlaku sisi miring kuadrat sama dengan jumlah kuadrat sisi-sisi lainnya. Secara umum, jika segitiga ABC siku-siku di C maka teorema Pythagoras dapat dinyatakan AB² = AC² + BC². Banyak buku menuliskan teorema ini sebagai c² = a² + b². Dengan c adalah sisi miring.
Rumus Pythagoras
Rumus Pythagoras didefinisikan dengan AB2 = BC2 + AC2 atau c2 = a2 + b2. Rumus tersebut dapat diinterpretasikan sebagai segitiga siku-siku ABC yang memiliki hipotenusa atau sisi miring (AB), sisi alas (BC) dan sisi tegak (AC). Pada Rumus Pythagoras berlaku panjang hipotenusa atau sisi miring (AB) dikuadratkan sama dengan penjumlahan kuadrat sisi alas (BC) dan sisi tegak (AC). Secara ilustrasi, Rumus Pythagoras dapat digambarkan seperti berikut:
Pembuktian Rumus Pythagoras
Berikut ini terdapat beberapa pembuktian rumus pythagoras, terdiri atas:
1. Teorema Pythagoras
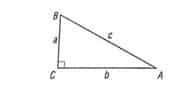
Jika ABC adalah segitiga siku-siku, maka panjang kuadrat sisi miring AC sama dengan penjumlahan panjang kuadrat dari sisi lainnya (AB dan BC)
AB2 = BC2 + AC2 atau c2 = a2 + b2
Bukti:
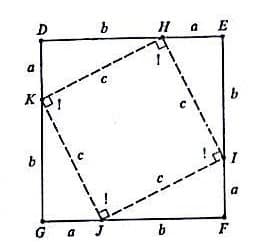
Teorema Pythagoras dapat dibuktikan tanpa menggunakan konsep similaritas. Diberikan ABC, dengan sisi kaki a, b dan sisi miring c. ambil □DEFG, dengan sisi a+b. didalam persegi tersebut bangun 4 segitiga yang kongruen, seperti gambar dibawah.
Maka KHI sudut siku-siku, karena sudut DHK dan sudut EHI adalah komplemennya. Semua sudut di □HIJK adalah siku-siku dan □HIJK adalah persegi.
Dengan menggunakan additivity postulate untuk luas area dari □DEFG sama dengan luas daerah □HIJK ditambah dengan luas dari 4 segitga siku-siku didalam persegi.
2. Teorema Converse Pythagoras
Jika segigitiga mempunyai sisi a, b dan c. a2 + b2 = c2, maka segitiga tersebut adalah segitiga siku-siku.
Bukti: a
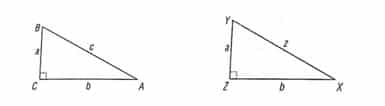
Diberikan segitiga ABC dengan sisi a, b, dan c dengan c2 = a2 + b2. Akan dibuktikan ABC adalah segitiga siku-siku. Perhatikan XYZ dengan sisi kaki a dan b.
Dengan menggunakan teorema Pythagoras a2 + b2 = z2
Tetapi di berikan a2 + b2 = c2
Dengan substitusi z2 = c2
Ambil akar positif di setiap sisi z = c
Maka, dengan SSS kongruen, ABC = XYZ jadi dengan menggunakan teorema CPCF, sudut C adalah sudut siku-siku dan ABC adalah segitiga siku-siku.
Contoh Soal Teorema Pythagoras
Berikut ini terdapat beberapa contoh soal teorema pythagoras, terdiri atas:
Soal No. 1
Diberikan sebuah segitiga siku-siku pada gambar berikut ini:
Tentukan panjang sisi miring segitiga!
Pembahasan:
AB = 6 cm
BC = 8 cm
AC = ……
Mencari sisi miring sebuah segitiga dengan teorema pythagoras:
Soal No. 2
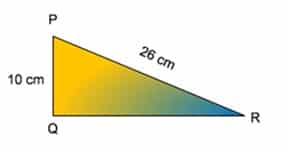
Diberikan sebuah segitiga siku-siku pada gambar berikut ini:
Tentukan panjang sisi alas segitiga!
Pembahasan:
PR = 26 cm
PQ = 10 cm
QR = ……
Menentukan salah satu sisi segitiga yang bukan sisi miring:
Soal No. 3
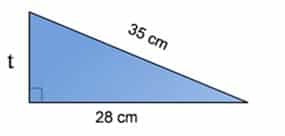
Sebuah segitiga siku-siku memiliki sisi miring sepanjang 35 cm dan sisi alas memiliki panjang 28 cm.
Tentukan luas segitiga tersebut!
Pembahasan:
Tentukan tinggi segitiga terlebih dahulu:
Luas segitiga adalah setengah alas dikali tinggi sehingga didapat hasil:
Soal No. 4
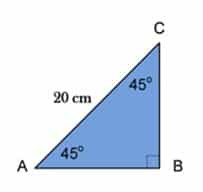
Perhatikan gambar segitiga berikut!
Tentukan panjang sisi AB!
Pembahasan:
Perbandingan panjang sisi-sisi pada segitiga siku-siku dengan sudut 45° adalah sebagai berikut:
Bandingkan sisi-sisi yang bersesuaian didapat:
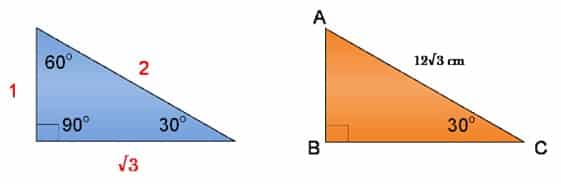
Berikutnya akan dibahas soal-soal segitiga yang menggunakan perbandingan dengan sudut-sudut 30o dan 60o
Soal No. 5
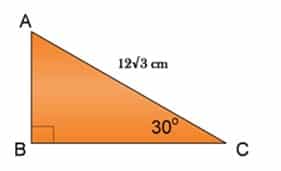
Perhatikan gambar segitiga ABC berikut ini!
Jika panjang AC 12√3 cm dan sudut C sebesar 30°, tentukan panjang AB dan panjang BC!
Pembahasan:
Tengok perbandingan sisi-sisi pada segitiga siku-siku yang mengandung sudut 30° dan 60° kemudian kita buat perbandingan dengan segitiga ABC:
Dari sisi-sisi yang bersesuaian diperoleh:
Demikianlah pembahasan mengenai Rumus Phytagoras – Pengertian, Sejarah, Dalil, Bunyi, Pembuktian dan Contoh Soal semoga dengan adanya ulasan tersebut dapat menambah wawasan dan pengetahuan anda semua, terima kasih banyak atas kunjungannya. 🙂 🙂 🙂