Pertidaksamaan Linear Satu Variabel
Pertidaksamaan Linear Satu Variabel – Pengertian, Rumus & Contoh – DosenPendidikan.Com – Pertidaksamaan linear satu variabel adalah kalimat terbuka yang dinyatakan dengan menggunakan tanda/lambang ketidaksamaan/pertidaksamaan dengan satu variable (peubah) berpangkat satu.

Pertidaksamaan Linear
-
Menemukan Konsep Pertidaksamaan Linear
Misal a, b adalah bilangan real, dengan a ≠ 0. Pertidaksamaan Linear Satu Variabel (PtLSV) adalah kalimat terbuka yang memiliki sebuah variabel yang dinyatakan dengan bentuk ax + b > 0 atau ax + b < 0 atau ax + b ≤ 0 atau ax + b ≥ 0.
- Menyelesaikan Pertidaksamaan Linear Satu Variabel (PtLSV)
Contoh
Rumah Ibu Suci dibangun di atas sebidang tanah berbentuk persegi panjang yang panjangnya 20 m dan lebarnya (6y – 1) m. Jika Luas tanah Ibu Suci tidak kurang dari 100 m2,
- berapakah lebar terkecil tanah ibu Suci?
- jika biaya untuk membangun rumah di atas tanah seluas 1m2 dibutuhkan uang Rp2.000.000,- Berapakah biaya terkecil yang harus disediakan Ibu Suci jika seluruh tanahnya dibangun?
Baca Juga : Rumus Prisma
Ingat kembali rumus Luas persegi panjang, Luas = panjang x lebar, Untuk tanah ibu Suci kita peroleh:
Luas = 20 × (6y – 1)
= 120y – 20 (ingatkah kamu bagaimana pengerjaannya? Jika Luas tanah ibu Suci tidak kurang dari 100 m2, maka model matematikanya adalah: 120y – 20 ≥ 100
Lebar tanah terkecil diperoleh untuk y paling kecil. Mengapa?
120y -20 ≥ 100
120y -20 + 20 ≥ 100 + 20 (kedua ruas ditambah 20)
120y ≥ 120 (kedua ruas dibagi 120)
y ≥ 1
Nilai y paling kecil dari penyelesaian y ≥ 1 adalah 1. Mengapa?
Lebar tanah terkecil diperoleh jika y = 1
Dengan mengganti y = 1 ke persamaan 6y – 1 diperoleh lebar = 6(1) – 1 = 5
Jadi lebar tanah terkecil Ibu Suci adalah 5 m.
Sifat-Sifat Pertidaksamaan
- Jika kedua ruas pertidaksamaan ditambah atau dikurang dengan sebuah bilangan maka tanda pertidaksamaan tetap.
- Jika kedua ruas pertidaksamaan dikali atau dibagi dengan sebuah bilangan positif maka tanda pertidaksamaan tetap.
- Jika kedua ruas pertidaksamaan dikali atau dibagi dengan sebuah bilangan negatif maka tanda pertidaksamaan harus diubah (< menjadi >, ≤ menjadi ≥, dan sebaliknya
Contoh :
3x + 6 ≥ 2x – 5
5q – 1 < 0
x dan q disebut variabel
Menyelesaikan Pertidaksamaan Linear Satu Variabel (PLSV)
- Menambah atau mengurangi kedua ruas (kanan kiri) dengan bilangan yang sama
Contoh :
Carilah penyelesaian x + 6 ≥ 8 jawab :
x + 6 – 6 ≥ 8 – 6
x ≥ 2
- Mengalikan atau membagi kedua ruas (kanan kiri) dengan bilangan yang Jika dikalikan atau dibagi bilangan negatif maka tanda pertidaksamaannya dibalik
Baca Juga : Persamaan Linear Satu Variabel
Contoh :
Carilah penyelesaian 2x – 4 < 10 jawab :
2x – 4 + 4 < 10 + 4
2x < 14

Carilah penyelesaian 3 – 4x ≥ 19 Jawab:
3 – 4x – 3 ≥ 19 – 3
-4x ≥ 16
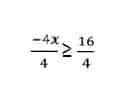
-x ≥ 4
-x . -1 ≤ 4 . -1 à kedua ruas dikalikan -1, sehingga lambang
pertidaksamaannya dibalik
x ≤ – 4
Pertidaksamaan adalah kalimat terbuka yang menggunakan lambing <, >, ≥, dan ≤ .
Contohnya bentuk pertidaksamaan : y + 7 < 7 dan 2y + 1 > y + 4
Pertidaksamaan linier dengan satu variable adalah suatu kalimat terbuka yang hanya memuat satu variable dengan derajad satu, yang dihubungkan oleh lambang <, >, ≥, dan ≤. Variablenya hanya satu yaitu y dan berderajad satu. Pertidaksamaan yang demikian disebut pertidaksamaan linier dengan satu variable (peubah).
Baca juga : 1 inci Berapa cm
Menentukan Himpunan Penyelesaian Pertidaksamaan Linier Satu variable
Sifat- sifat pertidaksamaan adalah :
- Jika pada suatu pertidaksamaan kedua ruasnya ditambah atau dikurang dengan bilangan yang sama, maka akan diperoleh pertidaksamaan baru yang ekuivalen dengan pertidaksamaan semula
- Jika pada suatu pertidaksamaan dikalikan dengan bilangan positif , maka akan diperoleh pertidaksamaan baru yang ekuivalen dengan pertidaksamaan semula
- Jika pada suatu pertidaksamaan dikalikan dengan bilangan negatif , maka akan diperoleh pertidaksamaan baru yang ekuivalen dengan pertidaksamaan semula bila arah dari tanda ketidaksamaan dibalik
- Jika pertidaksamaannya mengandung pecahan, cara menyelesaikannya adalah mengalikan kedua ruasnya dengan KPK penyebut-penyebutnya sehingga penyebutnya hilang .
Contoh :
- Tentukan himpunan penyelesaian 3x – 7 > 2x + 2 jika x merupakan anggota {1,2,3,4,… ,15}
Jawab :
3x – 7 > 2x + 2; x є {1, 2, 3, 4… 15}
3x –2x – 7 > 2x – 2x + 2 ( kedua ruas dikurangi 2x)
x – 7 > 2
x – 7 + 7 > 2 + 7 ( kedua ruas dikurangi7 )
x > 9
jadi himpunan penyelesaiannya adalah {x | x > 9 ; x bilangan asli ≤ 15}
HP = {10, 11, 12, 13, 14, 15}
Contoh :
Tentukan himpunan penyelesaian dari pertidaksamaan 3x – 1 < x + 3 dengan x variable pada himpunan bilangan cacah.
Jawab :
3x – 1 < x + 3
3x – 1+ 1 < x + 3 + 1 (kedua ruas ditambah 1 )
3x < x + 4
3x + (-x) < x + (-x) +4 (kedua ruas ditambah – x)
2x < 4
X < 2
Karena x anggota bilangan cacah maka yang memenuhi x < 2 adalah x = 0 atau x = 1
Jadi himpunan pnyelesaiannya adalah { 0,1 } .
Dalam garis bilangan, grafik himpunan penyelesaiannya adalah sebagai berikut.
-1 0 1 2 3 4 5
Baca Juga : Persamaan Linear Dua Variabel
Penyelesaian
Contoh :
x + < 6 +
x < 6 + –
x < 4 +
x – < 4
– < 4
< 4
-x < 4 . 6
x > -24
Contoh :
Sebuah perahu angkut dapat menampung dengan berat tidak lebih dari 1 ton . jika sebuah kotak beratnya 15 kg, maka berapa paling banyak kotak yang dapat diangkut oleh perahu ?
Jawab :
Kalimat matematika : 15 kg x ≤ 1 ton
Penyelesaian : 15 kg x ≤ 1 .500 kg
x ≤ 1 .500 kg
15 kg
x ≤ 100
jadi perahu paling banyak mengangkut 100 kotak.
Baca Juga : 1 Hektar Berapa Meter
Latihan
Pehatikan gambar atau kalimat berikut :
- Gambar disamping adalah rambu lalu lintas. Artinya adalah kendaraan yang lewat di jalan itu kecepatannya tidak boleh lebih dari 60 km/jam ( kecepatannya maksimum 60 km/ jam )
- Daya angkut 800 kg artinya muatan maksimum yang boleh diangkut mobil tersebut 800 kg. Dengan kata lain muatan mobil tersebut harus kurang dari atau 800 kg sama dengan 800 kg
- Usia pemain sepak bola yunior tidak boleh lebih dari 18 tahun.
- Kriteria kelulusan siswa SMP tahun 2007 adalah nilai ujian nasional tidak boleh kurang dari 4,25
Kerjakan dengan teman sebangku !
Jawab pertanyaan berikut dengan memperhatikan gambar atau kalimat di atas :
- Jika v menyatakan kecepatan mobil w menyatakan daya angkut u menyatakan usia n menyatakan nilai. Tulislah syarat untuk v, w, u, dan n dalam simbol matematika !
- Perhatikan jawaban anda no. 1
- Apakah setiap syarat yang anda tulis memuat variabel ?
- Berapa banyak variabel pada setiap syarat ?
- Berapa pangkat dari variabelnya ?
- Apakah dari syarat- syarat pada soal no. 1 merupakan pertidaksamaan linear satu variabel
- Tulislah dalam simbol matematika dari kalimat berikut :
- Berat badan dari petinju kelas berat adalah lebih dari 125 kg
- Daya tahan hidup Bola lampu maksimum 1440 jam
- Untuk menjadi anggota DPR, usia minimal adalah 21 tahun
- Sebuah negara dikatakan miskin jika pendapat kotornya ( GNP ) kurang dari $300.000/ tahun
- Seorang pilot harus memiliki tinggi badan minimal 170 cm.
Mengenal PtLSV dalam berbagi bentuk dan variabel
Masalah
Ricko mempunyai 5 kantong bola, masing- masing kantong isinya sama. Ayahnya memberi lagi 12 biji, teryata banyak bola Ricko sekarang lebih dari 70. Bila banyak bola tiap kantong adalah x biji, maka kalimat di atas jika ditulis dalam kalimat matematika menjadi :
5x + ……… > ……….
- Ada berapa variabelnya ?
- Berapa pangkat dari variabelnya ?
- Apakah kalimat itu merupakan kalimat terbuka ?
- Tanda hubung apa yang dipakai dalam kalimat itu ?
- Apakah kalimat itu merupakan pertidaksamaan linear dengan satu variabel ?
Latahian
- Perhatikan kalimat matematika berikut
- 2x – 3 < 7 f. 5k + 6 ≤ 3 (4k – 10)
- 4n + 2 = 8 g. 2b – 1 < 5b
- x + y ≥ 5 h. 4p < 6p – 11
- a2 < 49 i. 4 > -1
- 7t + 1 > 2t + 6
Dari kalimat di atas manakah yang merupakan PtLSV dan mana yang bukan PtLSV ? Jika bukan berikan alasannya !
- Buatlah 5 contoh, PtLSV dalam berbagai bentuk dan variabel.
Demikian penjelasan artikel diatas tentang Pertidaksamaan Linear Satu Variabel – Pengertian, Rumus & Contoh semoga dapat bermanfaat bagi pembaca setia DosenPendidikan.Com