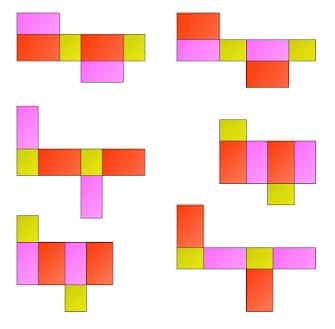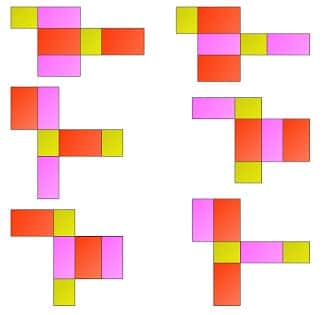Pengertian Balok
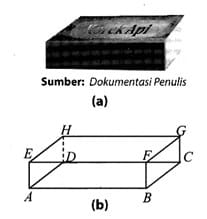
Jaring Jaring Balok -Pengertian, Rumus, Ciri, Unsur & Gambarnya– DosenPendidikan.Com– Perhatikan gambar kotak korek api pada Gambar 8.12(a). jika kotak korek api tersebut digambarkan secara geometris, hasilnya akan tampak seperti pada Gambar 8.12(b). bangun ruang ABCD.EFGH pada gambar tersebut memiliki tiga pasang sisi berhadapan yang sama bentuk dan ukurannya, dimana setiap sisinya berbentuk persegipanjang. Bangun ruang seperti ini disebut balok. Berikut ini adalah unsur-unsur yang dimiliki oleh balok ABCD.EFGH pada Gambar 8.12(b).
- Sisi/Bidang
Sisi balok adalah bidang yang membatasi suatu balok. Dari gambar 8.12(b), terlihat bahwa balok ABCD.EFGH memiliki 6 buah sisi berbentuk persegipanjang. Keenam sisi tersebut adalah ABCD (sisi bawah), EFGH (sisi atas), ABFE (sisi depan), DCGH (sisi belakang), BCGF (sisi samping kiri), dan ADHE (sisi samping kanan). Sebuah balok memiliki tiga pasang sisi yang berhadapan yang sama bentuk dan ukurannya. Ketiga pasang sisi tersebut adalah ABFE dengan DCGH, ABCD dengan EFGH, dan BCGF dengan ADHE.
- Rusuk
Sama seperti dengan kubus, balok ABCD.EFGH memiliki 12 rusuk. Coba perhatikan kembali Gambar 8.12(b) secara seksama. Rusuk-rusuk balok ABCD,EFGH adalah AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, dan HD.
- Titik Sudut
Dari Gambar 8.12, terlihat bahwa balok ABCD.EFGH memiliki 8 titik sudut, yaitu A, B, C, D, E, F, G, dan H. Sama halnya dengna kubus, balok pun memiliki istilah diagonal bidang, diagonal ruang, dan bidang diagonal.
- Diagonal Bidang
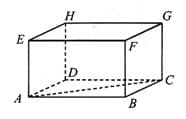
Coba kamu perhatikan Gambar 8.13. Ruas garis AC yang melintang antara dua titik sudut yang saling berhadapan pada suatu bidang, yaitu titik sudut A dan titik sudut C, dinamakan diagonal bidang balok ABCD.EFGH. coba kamu sebutkan diagonal bidang yang lain dari balok pada gambar 8.13.
Baca Juga : Jaring-Jaring Kubus
- Diagonal Ruang
Ruas garis CE yang menghubungkan dua titik sudut C dan E pada balok ABCD.EFGH seperti apda Gambar 8.14 disebut diagonal ruang balok tersebut. Jadi, diagonal ruang terbentuk dari ruas garis yang menghubungkan dua titik sudut yang saling berhadapan di dalam suatu bangun ruang.
- Bidang Diagonal
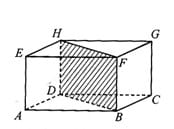
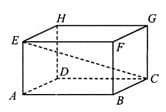
Sekarnag, perhatikan balok ABCD.EFGH pada Gambar 8.15. Dari gambar tersebut terlihat dua buah diagonal bidang yang sejajar, yaitu diagonal bidang HF dan DB. Kedua diagonal bidang tersebut beserta dua rusuk balok yang sejajar, yaitu DH dan BF membentuk sebuah bidang diagonal. Bidang BDHF adalah bidang diagonal balok ABCD.EFGH.
Ciri-Ciri Balok
Balok memiliki sifat yang hampir sama dengan kubus. Amatilah balok ABCD.EFGH pada gambar disamping. Berikut ini akan diuraikan sifat-sifat balok.
- Sisi-sisi balok berbentuk persegi panjang. Coba kamu perhatikan sisi ABCD, EFGH, ABFE, dan seterusnya. Sisi-sisi tersebut memiliki bentuk persegipanjang. Dalam balok, minimal memiliki dua pasang sisi yang berbentuk peregipanjang.
- Rusuk-rusuk yang sejajar memiliki ukuran sama panjang. Perhatikan rusuk-rusuk balok pada gambar disamping Rusuk-rusuk yang sejejar seperti AB, CD, EF dan GH memiliki ukuran yang sama panjang begitu pula dengan rusuk AE, BF, CG, dan DH memiliki ukuran yang sama panjang.
- Setiap diagonal bidang pada sisi yang berhadapan memiliki ukuran sama panjang. Dari gambar terlihat bahwa panjang diagonal bidang pada sisi yang berhadapan, yaitu ABCD dengan EFGH, ABFE dengan DCGH, dan BCFG dengan ADHE memiliki ukuran yang sama panjang
- Setiap diagonal ruang pada balok memiliki ukuran sama panjang. Diagonal ruang pada balok ABCD.EFGH, yaitu AG, EC, DF, dan HB memiliki panjang yang sama.
- Setiap bidang diagonal pada balok memiliki bentuk persegipanjang. Coba kamu perhatikan balok ABCD.EFGH pada gambar. Bidang diagonal balok EDFc memiliki bentuk persegipanjang. Begitupula dengna bidang diagonal lainnya.
Baca Juga : Transformasi Geometri
Jaring Jaring Balok
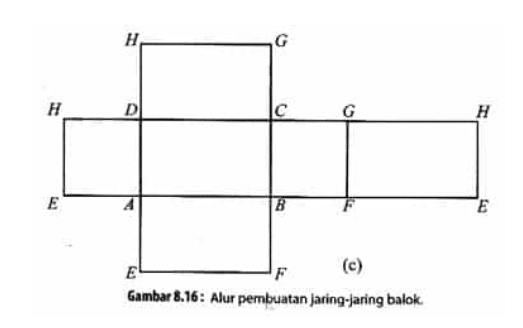
Sama halnya dengna kubus, jaring-jaring balok diperoleh dengan cara membuka balok tersebut sehingga terlihat seluruh permukaan balok. Coba perhatikan alur pembuatan jaring-jaring balok yang digambarkan pada Gambar 8.16.
Jaring-jaring balok yang diperoleh pada Gambar 8.16(c) tersusun atas rangkaian 6 buan persegipanjang. Rangkaian tersebut terdiri atas tiga pasang persegipanjang yang setiap pasangnya memiliki bentuk dan ukuran yang sama. Terdapat berbagai macam bentuk jaring-jaring balok. Diantaranya adalah sebagai berikut.
Luas Permukaan Balok
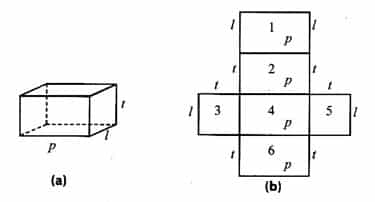
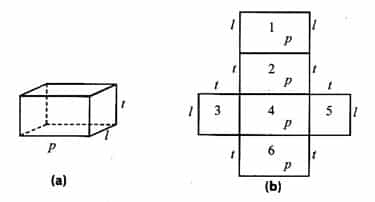
Cara menghitung luas permukaan balok sama dengan cara menghitung luas permukaan kubus, yaitu dengan menghitung semua luas jaring-jaringnya. Coba perhatikan gambar berikut.
Misalkan, rusuk-rusuk pada balok diberi nama p (panjang), l (lebar), dan t (tinggi) seperti pada gambar. Dengan demikian, luas permukaan balok tersebut adalah:
Luas Permukaan balok = Luas persegipanjang 1 + luas persegipanjang 2 +
Luas persegipanjang 3 + luas persegipanjang 4 +
Luas persegipanjang 5 + luas persegipanjang 6
= (p x l) + (p x t) + (l x t) + (p x l) + (l x t) + (p x t)
= (p x l) + (p x l) + (l x t) + (l x t) + (p x t) + (p x t)
= 2(p x l) + 2(l x t) + 2(p x t)
= 2(p x l) + (l x t) + (p x t)
= 2 (pl + lt + pt)
Baca Juga : Pertidaksamaan Nilai Mutlak
Jadi, luas permukaan balok dapat dinyatakan dengan rumus sebagai berikut.
Volume Balok
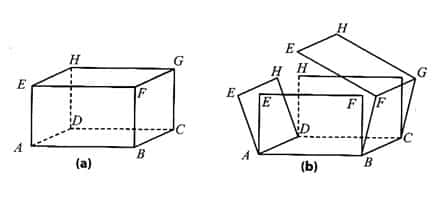
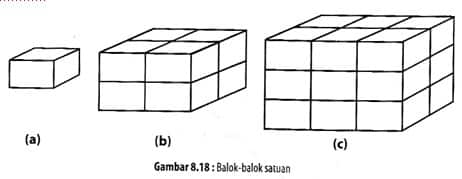
Proses penurunan rumus balok memiliki cara yang sama seperti pada kubus. Caranya adalah dengan menentukan satu balok satuan yang dijadikan acuan untuk balok yang lain. Proses ini digambarkan pada Gambar 8.18.
Gambar 8.18 menunjukkan pembentukan berbagai balok dari balok satuan. Gambar 8.18(a) adalah balok satuan. Untuk membuat balok seperti pada Gambar 8.18(b), diperlukan 2 x 1 x 2 = 4 balok satua, sedangkan untuk membuat balok seperti pada gambar 8.18(c) diperlukan 2 x 2 x 3 = 12 balok satuan. Hal ini menunjukkan bahwa volume suatu balok diperoleh dengan cara mengalikan ukuran panjang, lebar, dan tinggi balok tersebut.
Gambar Jaring Jaring Balok
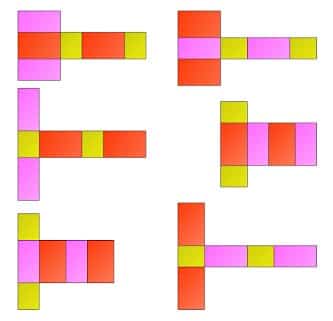
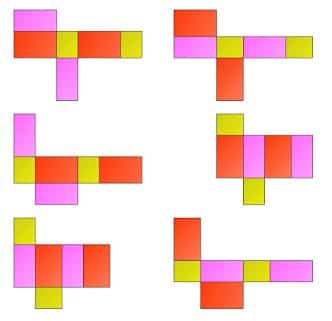
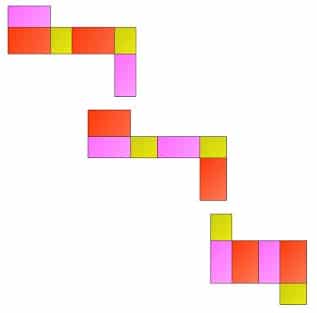
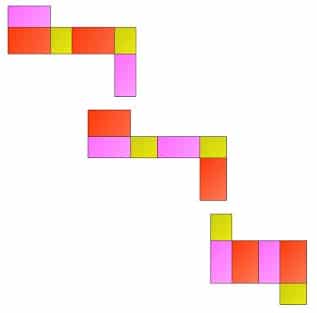
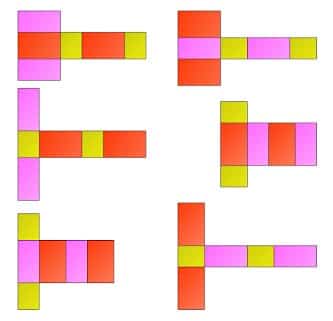
Jaring-jaring balok lebih banyak dan variatif jika kita bandingkan dengan jaring-jaring pada kubus, Hal ini dikarenakan balok sisi-sisinya terdiri atas bangun datar persegi panjang. Sama seperti pada jaring-jaring kubus jaring-jaring balok juga didapat dengan membuka bangun ruang balok sehingga diperoleh seluruh permukaan balok.
Berikuti ini adalah 54 contoh gambar jaring-jaring balok, silahkan kamu simak selengkapnya.


Baca Juga : Sin Cos Tan





Baca Juga : Integral Trigonometri




Sekian penjelasan artikel tentang Jaring Jaring Balok -Pengertian, Rumus, Ciri, Unsur & Gambarnya semoga bermanfaat bagi pembaca setia DosenPendidikan.Com