Distribusi Frekuensi Adalah – Pengertian, Relatif, Jenis & Contoh – Untuk pembahasan kali ini kami akan mengulas mengenai Distribusi Frekuensi yang dimana dalam hal ini meliputi Jenis dan Penyusunan, nah agar lebih dapat memahami dan mengerti simak ulasan selengkapnya dibawah ini.
Pengertian Distribusi Frekuensi
Data yang telah diperoleh dari suatu penelitian yang masih berupa data acak yang dapat dibuat menjadi data yang berkelompok yaitu data yang telah disusun ke dalam kelas-kelas tertentu. Daftar yang memuat data berkelompok disebut distribusi frekuensi atau tabel frekuensi.
- Menurut Hasan (2009)
Distribusi Frekuensi adalah Susunan data menurut kelas-kelas interval tertentu atau menurut katagori tertentu dalam sebuah daftar.
- Menurut Riduwan (2003)
Distribusi frekuensi adalah Penyusunan suatu data mulai dari terkecil sampai terbesar yang membagi banyaknya data kedalam beberapa kelas. Kegunaan data yang masuk dalam distribusi frekuensi adalah Untuk memudahkan data dalam penyajian, mudah dipahami, dan mudah dibaca sebagai informasi, pada gilirannya digunakan untuk perhitungan membuat gambar statistik dalam berbagai bentuk penyajian data.
Baca Juga :
Jenis-Jenis Distribusi Frekuensi
Distribusi frekuensi memiliki jenis-jenis yang berbeda untuk setiap kriterianya. Berdasarkan kriteria tersebut distribusi frekuensi dapat dibedakan tiga jenis “Hasan, 2001”.
Distribusi Frekuensi Biasa
Distribusi frekuensi yang berisikan jumlah frekuensi dari setiap kelompok data. Distribusi frekuensi ada dua jenis yaitu distribusi frekuensi numerik dan distribusi frekuensi peristiwa atau kategori.
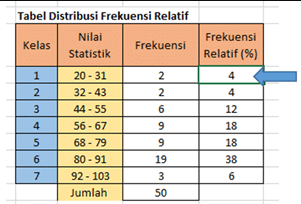
Distribusi Frekuensi Relatif
Distribusi frekuensi yang berisikan nilai-nilai hasil bagi antara frekuensi kelada dan jumlah pengamatan. Distribusi frekuensi relatif menyatakan proporsi data yang berada pada suatu kelas interval, distribusi frekuensi relatif pada suatu kelas didapatkan dengan cara membagi frekuensi dengan total data yang ada dari pengamatan atau observasi.
Distribusi Frekuensi Kumulatif
Distribusi frekuensi yang berisikan frekuensi kumulatif “frekuensi yang dijumlahkan”, distribusi frekuensi kumulatif memiliki kurva yang disebut ogif. Ada dua macam distribusi frekuensi kumulatif yaitu distribusi frekuensi kumulatif kurang dari dan distribusi frekuensi lebih dari.
Baca Juga : Efektivitas Adalah
Bagian-Bagian Distribusi Frekuensi
Menurut Hasan (2009) bagian-bagian distribusi frekuensi adalah sebagai berikut :
- Kelas-kelas
Kelas adalah kelompok nilai data
- Batas Kelas
Batas kelas adalah nilai-nilai yang membatasi kelas yang satu dengan kelas yang lain. Ada dua batas kelas yaitu :
- Batas bawah kelas terdapat disebelah kiri deretan kelas
- batas atas kelas terdapat disebelah kanan deretan kelas
- Tepi Kelas
Terpi kelas adalah batas kelas yang tidak memiliki lubang untuk angka tertentu antara kelas yang satu dengan kelas yang lain.
Tepi kelas ini kegunaanya waktu pembuatan histogram. Apabila ujung atas interval kelas pertama ditambah ujung bawah interval kedua dan dikalikan setengah, maka hasil tersebut dinamakan tepi kelas, atau ujung bawah interval kelas dikurangi 0,5; 0,05 bahkan 0,005 tergantung ketelitian data yang dibuat oleh peneliti dan diujung kelas atas ditambah 0,5; 0,05; 0,005 maka nilai itu dinamakan batas kelas.
- Titik tengah kelas
Adalah nilai data yang terletak ditengah-tengah kelas
Titik tengah kelas = ½(batas atas kelas + batas bawah kelas)
- Interval
adalah selang yang memisahkan kelas yang satu dengan kelas yang lain
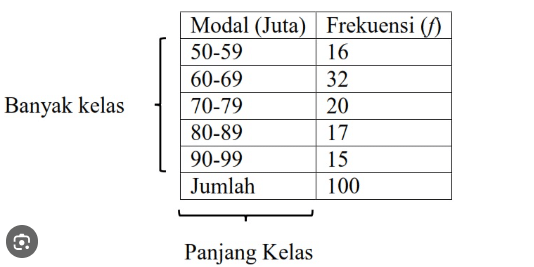
- Panjang interval kelas
Adalah jarak antara tepi atas kelas dan tepi bawah kelas
- Frekuensi kelas
Adalah banyaknya data yang termasuk kedalam kelas tertentu. Contoh :
Baca Juga : Pengertian, Konferensi Tingkat Tinggi Dan KTT Non-Blok
Dari distribusi frekuensi diatas :
- Banyaknya kelas adalah 7
- Batas kelas-kelas adalah 9, 21, 22, 34, …
- Batas bawah kelas-kelas adalah 9, 22, 35, 48, 61, 74, 87
- Batas atas kelas-kelas adalah 21, 34, 47, 60, 73, 86, 99
- Tepi bawah kelas adalah 8,5; 21,5; 34,5; 47,5; 60,5; 73,5; 86,5
- Tepi atas kelas adalah 21,5; 34,5; 47,5; 60,5; 73,5; 86,5; 99,5
- Titik tengah kelas adalah 15, 28, 41, 54, 67, 80, 93
- Interval Kelas adalah 9-21, 22-34, 35-47, 48-60, 61-73, 74-86, 87-99.
- Panjang Interval kelas-kelas masing-masing 13.
- Frekuensi kelas-kelas adalah 3, 4 ,4 ,8 ,12 ,23 ,6.
Penyusunan Distribusi Frekuensi
- Mengurutkan data dari yang terkecil ke yang terbesar
- Tentukan Range atau jangkauan data (R) Jangkauan = data terbesar – data terkecil
- Tentukan banyak kelas (k) Rumus Sturgess :
k=1+3,3 log n - Tentukan panjang interval kelas (i)
i = Jangkauan / banyak kelas - Batas bawah kelas pertama
Batas bawah kelas pertama biasanya dipilih dari data terkecil atau data terkecil yang berasal dari pelebaran jangkauan (data yang lebih kecil dari data terkecil) dan selisihnya harus kurang dari panjang interval kelasnya. - Menuliskan frekuensi kelas secara melidi dalam kolom turus atau tally (sistem turus) sesuai banyaknya data.
Contoh :
- Membuat tabel distribusi frekuensi dengan cara memindahkan semua angka frekuensi (f)
Baca Juga : 6 Pengertian Polotik Dan Ilmu Politik Menurut Para Ahli
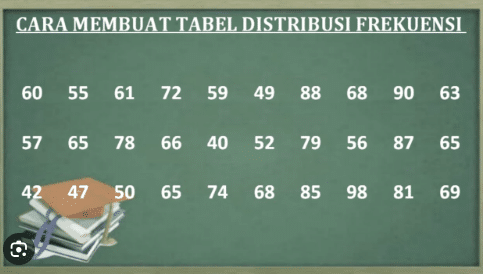
Contoh Membuat Tabel Distribusi Frekuensi
Data hasil ujian akhir Mata Kuliah Statistika dari 60 orang mahasiswa
23 60 79 32 57 74 52 70 82 36
80 77 81 95 41 65 92 85 55 76
52 10 64 75 78 25 80 98 81 67
41 71 83 54 64 72 88 62 74 43
60 78 89 76 84 48 84 90 15 79
34 67 17 82 69 74 63 80 85 61
Buatlah daftar distribusi frekuensi dari data diatas : Penyelesaian :
- Urutkan data
10 32 43 55 62 67 72 76 79 81 84 89
15 34 48 57 63 67 74 76 79 81 84 90
17 36 52 60 64 69 74 77 80 82 85 92
23 41 52 60 64 70 74 78 80 82 85 95
25 41 54 61 65 71 75 78 80 83 88 98
- Jangkauan (R) = 98 – 10 = 88
- Banyak kelas (k) = 1 + 3,3 log 60 = 6,8 ≈ 7
- Lebar interval kelas (i) = 88 / 7 = 12,5 ≈ 13
- Batas kelas pertama, misalnya diambil 9
- Menuliskan frekuensi secara melidi / turus
- Membuat tabel distribusi frekuensi dengan cara memindahkan semua angka frekuensi (f)
Histogram, Poligon Frekuensi Dan Kurva
- Histogram Dan Poligon Frekuensi
Histogram dan poligon frekuensi adalah dua grafik yang sering digunakan untuk menggambarkan distribusi frekuensi. Histogram merupakan grafik batang dari distribusi frekuensi dan poligon frekuensi merupakan grafik garisnya.
Pada histogram, batang-batangnya saling melekat atau berimpitan, sedang poligon frekuensi dibuat dengan cara menarik garis dari satu titik tengah batang histogram ke titik tengah batang histogram yang lain. Agar diperoleh poligon tertutup, harus dibuat dua kelas baru dengan panjang kelas sama dengan frekuensi nol pada kedua ujungnya. Pembuatan dua kelas baru itu diperbolehkan karena luas histogram dan poligon yang tertutup sama. Pada pembuatan histogram digunakan sistem salib sumbu. Sumbu mendatar (sumbu X) menyetakan interval kelas (tepi bawah dan tepi atas masing- masing kelas) dan sumbu tegak (sumbu Y) menyatakan frekuensi.
Baca Juga : “Dividen” Pengertian Menurut Para Ahli & ( Jenis – Prosedur Pembayaran )
Contoh Data hasil ujian akhir Mata Kuliah Statistika dari 60 orang mahasiswa
Kurva Frekuensi
Kurva distribusi frekuensi disingkat kurva frekuensi yang telah dihaluskan mempunyai berbagai bentuk dengan ciri-ciri tertentu. Bentuk-bentuk kurva distribusi frekuensi asalah sebagai berikut :
Baca Juga : “Kemasan” Pengertian & ( Fungsi – Tujuan – Jenis )
Jenis-Jenis Distribusi Frekuensi
Distribusi Frekuensi Biasa
Adalah distribusi yang hanya berisikan jumlah frekuensi dari setiap kelompok. Ada 2 yaitu :
- Distribusi frekuensi numerik
Adalah distribusi frekuensi yang pembagian kelasnya dinyatakan dalam angka.
- Distribusi frekuensi peristiwa
Adalah distribusi yang pembagian kelasnya dinyatakan berdsarkan golongan data yang ada.
Distribusi Frekuensi Mahasiswa Pendidikan Matematika
Distribusi Frekuensi Relatif
Distribusi frekuensi relatif adalah distribusi frekuensi yang berisikan nilai- nilai hasil bagi antara frekuensi kelas dan jumlah pengamatan yang terkandung dalam kumpulan data yang berdistribusi tertentu distribusi frekuensi relatif dapat dirumuskan :

Frekuensi relatif kadang-kadang dinyatakan dalam bentuk perbandingan, desimal, ataupun persen. Contoh Distribusi Frekuensi Relatif Nilai Ujian Akhir Mata Kuliah Statistika
Baca Juga : “Biaya” Pengertian – Jenis & ( Berdasarkan Tujuan – Berdasarkan Perilaku )
Distribusi Frekuensi Kumulatif
Distribusi frekuensi kumulatif adalah distribusi frekuensi yang berisikan frekuensi kumulatif. Frekuensi kumulatif adalah frekuensi yang dijumlah. Distribusi frekuensi kumulatif memiliki grafik atau kurva yang disebut OGIF. Pada ogif dicantumkan frekuensi kumulatifnya dan digunakan nilai batas kelas.
Ada dua macam Distribusi frekuensi kumulatif, yaitu :
- Distribusi Frekuensi Kumulatif Kurang Dari
Distribusi frekuensi kumulatif kurang dari adalah distribusi frekuensi yang memuat jumlah frekuensi yang memiliki nilai kurang dari nilai batas kelas suatu interval tertentu.
- Distribusi Frekuensi Kumulatif Lebih Dari
Distribusi frekuensi kumulatif lebih dari adalah distribusi frekuensi yang memuat jumlah frekuensi yang memiliki nilai lebih dari nilai batas kelas suatu interval tertentu.
CONTOH : Distribusi Frekuensi Kumulatif Kurang Dari
Distribusi Frekuensi Kumulatif Kurang Dari Untuk Nilai Ujian Akhir Mata Kuliah Statistika
Gambar distribusi frekuensi kumulatif kurang dari
Baca Juga : “Saluran Distribusi” Pengertian & ( Fungsi – Tingkatan – Bentuk )
CONTOH : Distribusi Frekuensi Kumulatif Lebih Dari
Distribusi Frekuensi Kumulatif Lebih Dari Untuk Nilai Ujian Akhir Mata Kuliah Statistika
Gambar distribusi frekuensi kumulatif lebih dari
Ogif Frekuensi Kumulatif Dari Untuk Nilai Ujian Akhir Mata Kuliah Statistika
Demikianlah pembahasan mengenai Distribusi Frekuensi Adalah – Pengertian, Relatif, Jenis & Contoh semoga dengan adanya ulasan tersebut dapat menambah wawasan dan pengetahuan kalian semua,, terima kasih banya. 🙂 🙂 🙂