Dalam fisika kita selalu menemukan hal yang berhubungan dengan besaran dan satuan, tahuakah kalian apa sebenarnya besaran itu,,?? Besaran didefinisikan sebagai sesuatu yang dapat diukur atau hasil pengukuran yang dinyatakan dalam bentuk nilai besaran “angka” dan satuan.
Setiap sesuatu yang ada disekitar kita yang dapat diukur, baik skala kecil maupun besar. Dasar satuan yang digunakan dalam besaran ialah Satuan Internasional “SI” yang merupakan satu hasil konferensi para ilmuan di Paris yang membahas tentang berat dan ukuran.
Dari pembahasan besaran ini, ditemukanlah yang disebut Dimensi. Sebenarnya apa sih dimensi itu..?? simak ulasan berikut ini.
Pengertian Dimensi Besaran
Dimensi besaran adalah penggambaran atau cara penulisan suatu besaran dengan menggunakan simbol “lambang” besaran pokok. Hal ini berarti dimensi suatu besaran menunjukkan cara besaran itu tersusun dari besaran-besaran pokok.
Apapun jenis satuan besaran yang digunakan tidak mempengaruhi dimensi besaran tersebut, misalnya satuan panjang dapat dinyatakan dalam m, cm, km, ft, keempat satuan ini mempunyai dimensi yang sama yakni L.
Pada sistem satuan internasional “SI” ada tujuah besaran pokok yang berdimensi, sedangkan dua besaran pokok tambahan tidak berdimensi, cara penulisan dimensi dari suatu besaran dinyatakan dengan lambang huruf tertentu dan diberiu kurung persegi.
Besaran Pokok
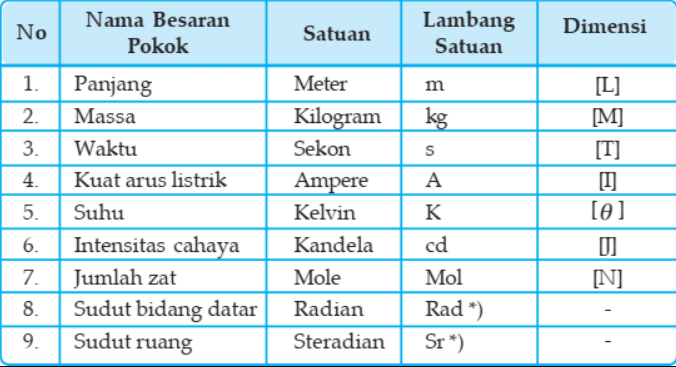
Besaran pokok adalah biasanya ditulis dengan huruf pertama dari nama be- saran yang bersangkutan, dalam bahasa Inggris. Contoh: dimensi untuk panjang (Inggris: length) adalah [L].
Berikut tabel besaran pokok beserta dimensinya:
Rumus Besaran Pokok
Berikut ini terdapat beberapa rumus besaran pokok, terdiri atas:
| NO | Besaran Pokok | Rumus |
| 1 | Luas | panjang x lebar |
| 2 | Volume | panjang x lebar x tinggi |
| 3 | Massa Jenis | massavolume |
| 4 | Kecepatan | perpindahan waktu |
| 5 | Percepatan | kecepatan waktu |
| 6 | Gaya | massa x percepatan |
| 7 | Usaha dan Energi | gaya x perpindahan |
| 8 | Impuls dan Momentum | gaya x waktu |
Besaran Turunan
Besaran turunan merupakan kombinasi dari dimensi besaran pokok, sesuai dengan cara besaran turunan tersebut diperoleh dari besaran pokok. Dimensi dari beberapa besaran turunan dalam mekanika ditunjukkan pada tabel Terlihat bahwa besaranmekanika merupakan gabungan dari tiga besaran pokok, yaitu massa, panjang, dan waktu.
Dimensi dari besaran turunan dapat disusun dari dimensi besaran-besaran pokok, berikut ini tabel besaran turunan:
Tidak hanya berpaku pada tabel diatas, cukup banyak besaran turunan lainnya yang dapat dibuat dimensinya untuk membuktikan kebenaran dari besaran atau persamaan tersebut. Seiring berjalannya waktu, perkembangan besaran turunan makin meningkat sehingga dapat dikatakan dimensi besaran turunan dapat terus diperbaharui.
Fungsi Dimensi
Jika dipahami dengan seksama, dapat diambil kesimpulan beberapa fungsi dari dimensi yaitu:
Dimensi Digunakan Untuk Membuktikan Kebenaran Suatu Persamaan. Pembelajaran ilmu fisika banyak bentuk-bentuk penjelasan sederhana untuk memudahkan seperti persamaan fisika. Bagaimana cara membuktikan kebenarannya..?? salah satunya ialah dengan analisa dimensional.
Analisis Dimensional
Analisis dimensional ialah suatu cara untuk menentukan satuan dari suatu besaran turunan, dengan cara memperhatikan dimensi besaran tersebut. Salah satu manfaat dari konsep dimensi ialah untuk menganalisis atau menjabarkan benar atau salahnya suatu persamaan “fungsi dimensi”, metode penjabaran dimensi atau analisis dimensi menggunakan aturan:
- Dimensi ruas kanan sama dengan dimensi ruas kiri.
- Setiap suku berdimensi sama.
Contoh Soal Dimensi Besaran
Contoh Ke-1
Sebuah benda yang bergerak diperlambat dengan perlambatan a yang tetap dari kecepatan vodan menempuh jarak sebesar s maka akan berlaku hubungan vo2=2aS. Buktikan kebenaran persamaan itu dengan analisa dimensional..!!!
Karena kedua ruas kiri dan kanan sama, artinya persamaannya kemungkinan besar benar.
Contoh Ke-2
Sebuah helikopter memiliki daya angkat P yang hanya bergantung pada berat beban total W (yaitu berat helikopter ditambah berat beban) yang diangkat, massa jenis udara ρ dan panjang baling-baling helikopter l.
- Gunakan analisa dimensi untuk menentukan ketergantungan P pada W , ρ, dan l.
- Jika daya yang dibutuhkan untuk mengangkat beban total W adalah P0, berapakah daya yang dibutuhkan untuk mengangkat beban total 2W ?
Penyelesaian:
a) Dari informasi soal didapat
P = CW αρβlγ
Dengan mengingat bahwa C adalah sebuah konstanta tidak berdimensi, dimensi da- ya P adalah [M ][L]2[T ]−3, dimensi gaya W adalah [M ][L][T ]−2, dimensi rapas jenis udara ρ adalah [M ][L]−3, sedang dimensi panjang l adalah [L]. Dengan demikian dapat diperoleh persamaan dimensi sebagai berikut
[M ][L]2[T ]−3 = .[M ][L][T ]−2Σα .[M ][L]−3Σβ ([L])γ .
Dengan mencocokan dimensi [T ], didapatkan
−3 = −2α atau α = 3.
2
Selanjutnya, dengan mencocokkan dimensi [M ] didapatkan
1 = α + β atau β = − 1.
2
Terakhir, dengan mencocokkan dimensi [L] didapatkan
2 = α − 3β + γ atau γ = −1.
Dengan demikian didapatkan persamaan akhir
P = CW 3/2ρ−1/2l−1.
b) Terlihat bahwa P W 3/2. Jika beban total W dinaikkan dua kali, maka daya baru P menjadi 23/2P0 = 2√2P0.
Contoh Ke-3
Periode revolusi planet
Periode revolusi (T ) dari sebuah planet yang berputar mengelilingi matahari dalam orbit lingkaran tergantung pada jari-jari orbit (r), massa matahari (M ), konstanta gravitasi (G), serta konstanta tak berdimensi C. Dengan menggunakan analisis dimensi, carilah Hukum ke-3 Keppler untuk gerakan planet.
Penyelesaian
Persamaan periode T dapat ditulis sebagai
T = CrαM βGγ,
yang dapat ditulis sebagai persamaan dimensi sebagai berikut
[T ] = [L]α [M ]β .[M ]−1 [L]3 [T ]−2Σγ .
Persamaan di atas memberi kita 3 persamaan linier, yaitu
1 = −2γ
0 = α + 3γ
0 = β − γ,
sehingga didapatkan γ = −1/2, β = −1/2 dan α = 3/2. Dengan demikian persamaan untuk periode adalah
T = Cr3/2M −1/2G−1/2.
Demikianlah pembahasan mengenai Dimensi Besaran – Pengertian, Rumus, Fungsi dan Contoh Soal semoga dengan adanya ulasan tersebut dapat menambah wawasan dan pengetahuan anda semua, terima kasih banyak atas kunjungannya.