Apa itu Belah Ketupat ??
Belah Ketupat – Rumus, Sifat, Ciri, Unsur Dan Contoh Soalnya – Belah Ketupat adalah segi empat yang dibentuk oleh dua gabungan segitiga samakaki yang diimpitkan pada alasnya.
Sifat-Sifat belah ketupat :
- Sisi-sisi pada belah ketupat sama panjang.
- Sudut-sudut yang berhadapan pada belah ketupat sama besar.
- Kedua diagonal belah ketupat saling membagi dua sama panjang dan saling tegak lurus.
- Diagonalnya tidak sama panjang.
Ciri – Ciri Balah Ketupat
- Mempunyai empat rusuk yang sama panjang
- Mempunyai dua buah sudut bukan siku-siku yang masing masing sama besar dengan sudut yang berada di hadapannya
- Mempunyai dua diagonal yang tidak sama panjang
- Mempunyai 2 simetri lipat dan dua simetri putar
Rumus Belah Ketupat
Belah ketupat adalah bangun datar dua dimensi yang dibentuk oleh empat buah rusuk yang sama panjang, dan memiliki dua pasang sudut bukan siku-siku yang masing-masing sama besar dengan sudut di hadapannya.
Luas Daerah Belah Ketupat
Untuk menghitung luas daerah belah ketupat ABCD dapat dicari dengan menggunakan rumus luas segitiga. Luas belah ketupat ABCD sama dengan luas segitiga ABD ditambah dengan luas segitiga CBD.
Luas belah ketupat ABCD
= Luas segitiga ABD + Luas segitiga CBD
= ( 1/2 x BD x OA) + ( 1/2 x BD x OC )
= 1/2 x [(BD x OA) + ( BD x OC)]
= 1/2 x [(OA + OC) x BD] dengan OA + OC = AC
Sehingga,
Luas belah ketupat ABCD = 1/2 x AC X BD
Dimana, AC = diagonal 1 dan BD = diagonal 2
Rumus Keliling Belah Ketupat
Rumus keliling dan luas belah ketupat sebagai berikut :
Pada gambar belah ketupat diatas mempunyai sisi AB, BC, CD dan AD. Jika panjang sisi belah ketupat s, maka AB=BC=CD=AD=s. Keliling belah ketupat ABCD adalah jumlah dari panjang semua sisinya yaitu AB+BC+CD+AD. Dengan rumus keliling belah ketupat adalah AB+BC+CD+AD= s+s+s+s = 4s
Sehingga rumus belah ketupat adalah:
Jika Belah Ketupat ABCD dengan sisi s dan Keliling K, maka K=4s
- Contoh soal 1
Jika panjang sisi belah ketupat adalah 15 cm, berapakah kelilingnya?
Jawab:
K = 4s = 4 x 15 = 60 cm
- Contoh soal 2
Pada gambar belah ketupat disamping, mempunyai keliling 48 cm, tentukan panjang sisinya !
Jawab:
Baca Juga : Volume Bola
- Rumus Luas Belah Ketupat
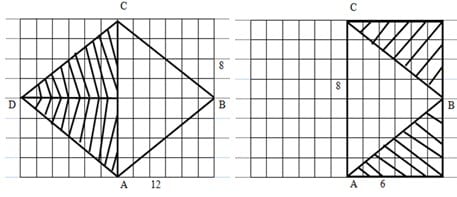
Setelah bagian yang diarsir dibagian atas dipindahkan ke bagian bawah terlihat bahwa:
Luas belah ketupat= ½ luas persegi panjang
Sehingga dapat ditulis:
Luas belah ketupat
- Contoh soal 1
Jika AC= 10 cm, BD=6 cm
Carilah luasnya!
Jawab:
Luas = ½ x diagonal1 x diagonal2
= ½ x 10 cm x 6 cm
= 30 cm2
- Contoh soal 2:
Jika luas belah ketupat adalah 96 cm2 dan diagonal 1 adalah 12 cm, berapakah diagonal 2 nya?
Jawab:
- L = ½ x diagonal1 x diagonal2
- 96 cm2 = ½ x 12 cm x d2
- 96 cm2 = 6 cm x d2
- d2 = 16 cm
Unsur-unsur pada belah ketupat :
- AB,BC,CD,dan AD dinamakan sisi belah ketupat ABCD.
- AC dan BD dinamakan diagonal belah ketupat ABCD.
Baca Juga : Rumus Volume Tabung
Contoh Soal
- Berapa besar sebuah diagonal jika diagonal yang lain besarnya 20 cm dan Luasnya 220 cm2 ?
Diket :
d1 : 20 cm d2 : ? Luas : 220 cm2
L = ½ x d1 x d2
220 = ½ x 20 x d2
d2 = 220 x 2 = 22 cm
20 x1
- Jika Sebuah Belah Ketupat memiliki diagonal 12 cm dan 14 cm . Berapakah besar luasnya?
Diket :
d1 = 12cm d2 = 14 cm
L = ½ x d1 x d2
=1/2 x 12 x 14
L = 84 cm2
Quiz
- Panjang diagonal belah ketupat PQRS ialah PR= 8 cm dan QS = ( x + 2) cm jika luas belah ketupat 48cm2 maka nilai x adalah….
- 4
- 8
- 10
- 16
- Yang merupakan sifat – sifat belah ketupat adalah…
- Diagonalnya sama panjang
- Besar sudutnya yang berhadapan 360 o
- Panjang sisinya sama panjang
- Panjang sisinya tidak sama
- Sebuah Belah Ketupat memiliki diaognal yang besarnya 32cm dan 13 cm berapakah luasnya…
- 208cm2
- 124 cm2
- 226cm2
- 152 cm2
Baca Juga : Rumus Trapesium
Sifat-sifat (Teorema)
Semua sisi pada setiap belah ketupat sama panjang.
Bukti :
Belah ketupat ABCD dibentuk dari dua buah segitiga sama kaki yang kongruen, yaitu ∆ ABC dan ∆ ADC.
∆ ABC ∆ ADC
AB = AD
BC = CD KONGRUEN (ss, ss, ss)
AC = AC
∆ ABC sama kaki, maka
AB = BC
∆ ADC sama kaki, maka
CD = AD
Maka : AB = AD = DC = AD (terbukti)
Pada setiap belah ketupat diagonalnya merupakan sumbu simetri.
Bukti :
- ∆ ABC sama kaki dengan AB = CB, BO merupakan sumbu simetri.
- ∆ ADC sama kaki dengan AD = DC, DO maerupakan sumbu simetri.
- < BOC dan < COD berpelurus, maka BD merupakan sumbu simetri.
- < BOC dan < BOA berpelurus, maka AC merupakan sumbu simetri.
- Jadi terbukti BD dan AC merupakan sumbu simetri.
- Pada setiap belah ketupat sudut-sudut yang berhadapan sama besar dan dibagi sama besar oleh diagonal-diagonalnya
Bukti :
- Cara I
- Letak belah ketupat ABCD dibalik menurut simetri BD
Maka < A→ < C sehingga :
< A = < C…..(1)
- Letak belah ketupat ABCD dibalik menurut sumbu simetri AC maka < B → < D sehingga < B = < D…..(2)
- Dari (1) dan (2), maka :
< A = < C, < B = < D (Terbukti)
- Cara II
∆ ABD ∆ CBD, maka :
< A = < C → BD = BD (berimpit)
Segitiga yang membentuk belah ketupat ABCD merupakan segitiga sama kaki, maka dalam ∆ ABD, < ABD = < ADB dan dalam ∆ CBD, < CBD = < CDB.
< ABD = < ADB → AD = AB
< CBD = < CDB → CD = CB
- ∆ BAC ∆ DAC, maka :
< B = < D → AC = AC (berimpit)
Segitiga yang membentuk belah ketupat ABCD merupakan segitiga sama kaki, maka dalam ∆ BAC, < BAC = < BCA dan dalam ∆ DAC, < DAC = < DCA.
< BAC = < BCA → BC = BA
< DAC = < DCA → CD = AD
Jadi, dalam belah ketupat ABCD terdapat < A = < C dan < B = < D. Sudut-sudut yang saling berhadapan dalam belah ketupat sama besar.
Pada setiap belah ketupat kedua diagonalnya saling membagi-dua sama panjang dan saling berpotongan tegak lurus.
Bukti :
Cara I
Misalkan O adalah titik tengah diagonal BD. Segitiga sama kaki ABD dibentuk dari dua segitiga siku-siku yang kongruen, yaitu ∆ AOB dan ∆ AOD dengan AO sebagai sumbu simetri ∆ ABD, BO = DO, < OAB = < OAD, dan < AOB = < AOD = 90o.
Baca Juga : Bilangan Prima Adalah – Pengertian, Rumus, Genap & Faktornya
Serupa dengan cara di atas, CO adalah sumbu simetri dari ∆ CBD, < OCB = < OCD, dan < COB = < COD = 90o.
Hal ini berarti < AOB + < COB = 2 x 90o = 180o
< AOB + < AOD = 2 x 90o = 180o.
Jadi, AC dan BD merupakan diagonal ketupat.
Karena BD diagonal belah ketupat ABCD yang diperoleh dari pemutaran ∆ ABD pada garis BD maka : A → C, O → O sehingga AO → CO. Hal ini berarti AO = CO.
Cara II
< A1 = < C2 (berseberangan dalam) → BO = DO
< A2 = < C1 (berseberangan dalam) → DO = BO
< B1 = < D2 (berseberangan dalam) → AO = CO
< B2 = < D1 (berseberangan dalam) → CO = AO
< AOB = < AOD = < AOD = < COD = 90o (berpenyiku)
< BOD = 180o (berpelurus)
< AOC = 180o (berpelurus)
< COD = < AOD = 90o
< BOD = < AOB + < AOD = 2 x < AOB = 2 x 90o = 180o
< AOC = < AOD + < COD = 2 x < AOD = 2 x 90o = 180o
Jadi, AC dan BD merupakan diagonal ketupat yang saling membagi-dua sama panjang dan saling berpotongan tegak lurus.
Baca Juga : Rumus Deret Geometri
- Berdasarkan Luas Jajar Genjang
Bukti :
- Karena belah ketupat merupakan jajar genjang, maka :
- L Belah Ketupat = alas x tinggi
- L = a x t
- Berdasarkan Luas Segitiga
Bukti :
Luas belah ketupat ABCD = L ∆ ABD + L ∆BDC
= ½ BD x OA + ½ BD x OC
= ½ BD (OA + OC)
= ½ BD x AC
BD dan AC merupakan diagonal
Sehingga dapat disimpulkan :
Luas Belah Ketupat ABCD = 1/2 x diagonal x diagonal
Demikianlah penjelasan artikel diatas tentang Belah Ketupat – Rumus, Sifat, Ciri, Unsur Dan Contoh Soalnya semoga bisa bermanfaat bagi pembaca setia DosenPendidikan.Com