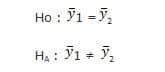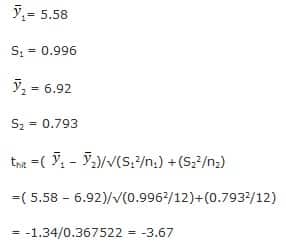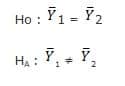DosenPendidikan.Com – Uji t dikembangkan oleh William Sealy Gosset. Dalam artikel publikasinya, ia menggunakan nama samaran Student, sehingga kemudian metode pengujiannya dikenal dengan uji t-student. William Sealy Gosset menganggap bahwa untuk sampel kecil, nilai Z dari distribusi normal tidak begitu cocok. Oleh karenanya, ia kemudian mengembangkan distribusi lain yang mirip dengan distribusi normal, yang dikenal dengan distribusi t-student.
Distribusi student ini berlaku baik untuk sampel kecil maupun sampel besar. Pada n ≥ 30, distribusi t ini mendekati distribusi normal dan pada n yang sangat besar, misalnya n=10000, nilai distribusi t sama persis dengan nilai distribusi normal (lihat tabel t pada df 10000 dan bandingkan dengan nilai Z).
Pemakaian uji t ini bervariasi. Uji ini bisa digunakan untuk objek studi yang berpasangan dan juga bisa untuk objek studi yang tidak berpasangan. Berikut contoh penggunaan uji t.
Uji t tidak berpasangan
Contoh kasus
Kita ingin menguji dua jenis pupuk nitrogen terhadap hasil padi
- Hipotesis
- Hasil penelitian tertera pada Tabel 1.
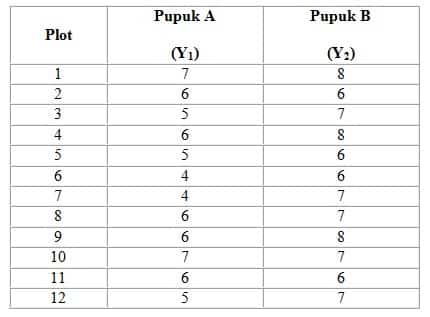
Tabel 1. Data hasil penelitian dua jenis pupuk nitrogen terhadap hasil padi (t/h)
- Data analisis adalah sebagai berikut
Hitunglah
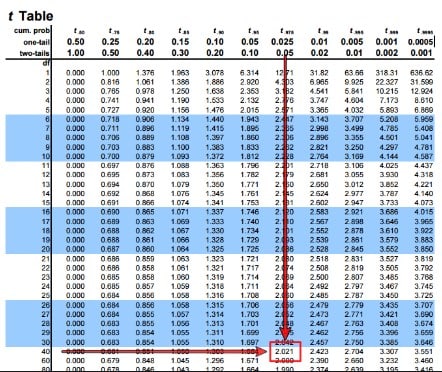
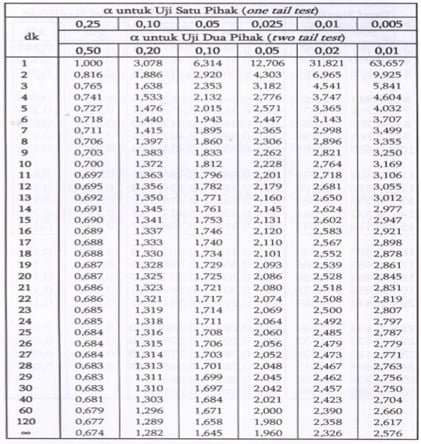
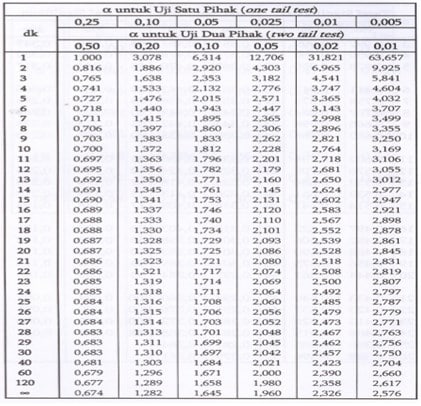
Setelah itu, kita lihat nilai t table, sebagai nilai pembanding. Cara melihatnya adalah sebagai berikut. Pertama kita lihat kolom α = 0.025 pada Tabel 2. Nilai α ini berasal dari α 0.05 dibagi 2, karena hipotesis HAkita adalah hipotesis 2 arah (lihat hipotesis). Kemudian, kita lihat baris ke 22. Nilai 22 ini adalah nilai df, yaitu n1+n2-2. Nilai n adalah jumlah ulangan, yaitu masing 12 ulangan. Akhirnya, kita peroleh nilai t table = 2.074.
Baca Juga : 1 inci Berapa cm

Tabel 2. Nilai t
- Kriteria Pengambilan Kesimpulan
Terima H0, jika thit| < t table, sebaliknya
Tolak H0, alias terima HA, jika thit| > t table
- Kesimpulan
Karena nila thit|= 3.67 (tanda minus diabaikan) dan nilai t table=2.074, maka kita tolak H0, alias kita terima HA. Dengan demikian, 1 ≠ 2, yaitu hasil padi yang dipupuk dengan pupuk A tidak sama dengan hasil padi yang dipupuk dengan pupuk B. Lebih lanjut, kita lihat bahwa rata-rata hasil padi yang dipupuk dengan pupuk B lebih tinggi daripada yang dipupuk dengan pupuk A. Dengan demikian, kita dapat menyimpulkan bahwa pupuk B nyata lebih baik daripada pupuk A untuk meningkatkan hasil padi.
Baca Juga : Persamaan Linear Satu Variabel
Uji t berpasangan
Uji t dikembangkan oleh William Sealy Gosset. Dalam artikel publikasinya, ia menggunakan nama samaran Student, sehingga kemudian metode pengujiannya dikenal dengan uji t-student. William Sealy Gosset menganggap bahwa untuk sampel kecil, nilai Z dari distribusi normal tidak begitu cocok.
Oleh karenanya, ia kemudian mengembangkan distribusi lain yang mirip dengan distribusi normal, yang dikenal dengan distribusi t-student. Distribusi student ini berlaku baik untuk sampel kecil maupun sampel besar. Pada n ≥ 30, distribusi t ini mendekati distribusi normal dan pada n yang sangat besar, misalnya n=10000, nilai distribusi t sama persis dengan nilai distribusi normal (lihat tabel t pada df 10000 dan bandingkan dengan nilai Z).
Pemakaian uji t ini bervariasi. Uji ini bisa digunakan untuk objek studi yang berpasangan dan juga bisa untuk objek studi yang tidak berpasangan. Berikut contoh penggunaan uji t.
Uji t berpasangan
Contoh kasus. Kita ingin menguji metode pembelajaran baru terhadap tingkat penguasaan materi ajar pada mahasiswa.
- Hipotesis
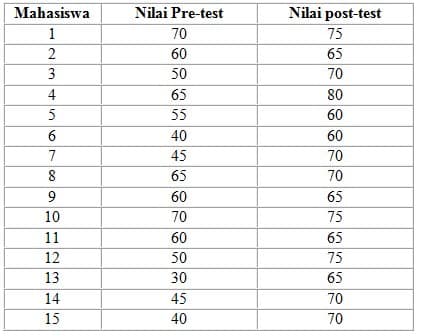
- Data hasil penelitian dari penggunaan metode pembelajaran baru adalah sebagaimana tertera pada Tabel 1.
Tabel 1. Data hasil penelitian dari penggunaan metode pembelajaran baru
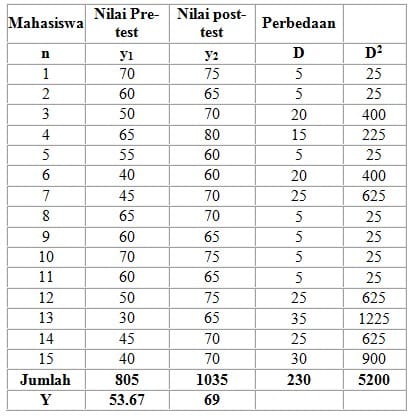
- Data analisis adalah sebagai berikut.
Tabel 2. Tabel analisis data
Baca Juga : Pertidaksamaan Linear Satu Variabel
Hitunglah
Setelah itu, kita lihat nilai t table, sebagai nilai pembanding. Cara melihatnya adalah sebagai berikut. Pertama kita lihat kolom α = 0.025 pada Tabel 3. Nilai α ini berasal dari α 0.05 dibagi 2, karena hipotesis HAkita adalah hipotesis 2 arah (lihat hipotesis). Kemudian, kita lihat baris ke 14. Nilai 14 ini adalah nilai df, yaitu n-1. Nilai n adalah jumlah mahasiswa, yaitu 15 orang. Akhirnya, kita peroleh nilai t table = 2.145.
t table = t α/2 (df) = t0.05/2 (n-1)=t0.025(15-1) = t0.025(14) = 2.145
Tabel 2. Nilai t
- Kriteria Pengambilan Kesimpulan
Terima H0, jika thit| < t table, sebaliknya
Tolak H0, alias terima HA, jika thit| > t table
Baca Juga :
- Kesimpulan
Karena nila |thit|= 5.431 (tanda minus diabaikan) dan nilai t table=2.145, maka kita tolak H0, alias kita terima HA. Dengan demikian,
![]()
Yaitu nilai pre-test tidak sama dengan nilai post-test. Lebih lanjut, kita lihat bahwa rata-rata nilai post-test lebih tinggi daripada nilai pre-test. Secara lengkap, kita dapat menyimpulkan bahwa metode pembelajaran baru secara nyata dapat meningkatkan pemahaman mahasiswa terhadap materi ajar yang diberikan.
Mencari Nilai Tabel t
Tabel t dapat dipergunakan untuk menguji rata-rata hitung populasi dalam sampel kecil. Proses pengujian hipotesa untuk sampel kecil tidak berbeda dengan sampel besar, yakni melalui beberapa tahapan sebagai berikut :
a) merumuskan hipotesa nol (Ho) dan hipotesa alternatif (Ha); b) menentukan nilai alpha (taraf nyata) apakah 1%, 5% atau pada taraf lainnya serta mengetahui titik kritis berdasarkan pada tabel t; c) menentukan uji statistik dengan menggunakan rumus uji-t; d) menentukan daerah keputusan yaitu daerah tidak menolak Ho dan daerah menolak Ho; dan e) mengambil keputusan untuk menolak dan menerima dengan membandingkan nilai alpha dengan nilai uji-t.
Satu Sisi
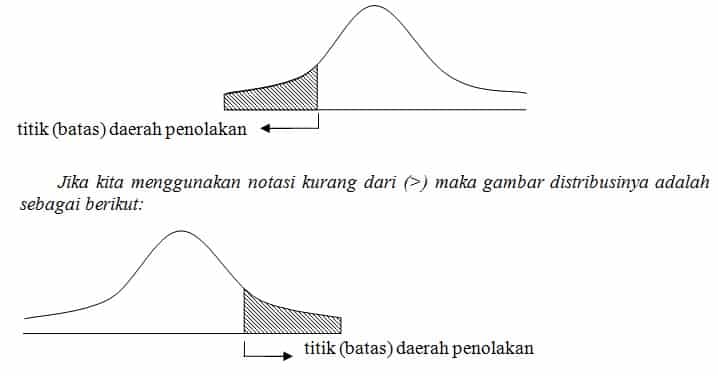
Sebagaimana dalam uji statistik untuk sampel besar (n>30), penggunaan notasi akan menentukan posisi daerah penolakan dalam gambar distribusi. Jika kita menggunakan notasi kurang dari (<) maka gambar distribusinya adalah sebagai berikut:
Tabel t digunakan untuk menentukan titik kritis (batas) daerah penolakan yang dalam distribusi menggunakan notasi alpha (a), dan juga nilai dari hasil perhitungan statistik, sehingga kita bisa mengambil kesimpulan. Pada tabel t, nilai kritis dalam uji statistik satu sisi adalah: t (a , v) ; dengan v = n-1
Contoh
Dalam suatu penelitian ditentukan bahwa n = 4 dan nilai alpha 0,01 (1%) maka untuk mengetahui nilai kritis dalam distribusi yang ditunjukkan dengan tabel t untuk satu sisi adalah sebagai berikut:
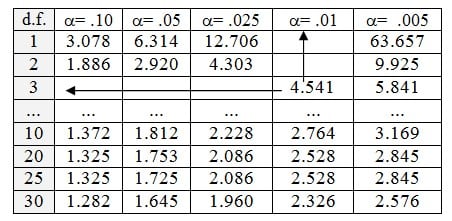
- Langkah pertama: Setelah merumuskan hipotesa nol dan hipotesa alternatif (Ho, Ha) serta menentukan nilai alpha, Tabel t digunakan untuk menentukan titik kritis dengan formula t = (a , v); dengan v = n – 1 untuk uji statistik satu sisi. Setelah ditentukan nilai alpha adalah 0,01 maka langkah selanjutnya adalah menentukan derajat bebas (v) yang diperoleh dari n – 1. Jumlah n = 4, jadi 4 – 1 = 3.
- Langkah kedua: perhatikan tabel t (dalam BMP lihat halaman 9.22). Diketahui bahwa df = 3, maka cari angka 3 di garis paling kiri kemudian tarik ke kanan sampai kolom a = 0,01 akan didapat nilai t adalah 4,541. Dengan cara yang sama dapat dicari nilai kritis untuk alpha (a) dan derajat bebas (v) yang lain.
- Langkah ketiga: melakukan uji statistik t dengan rumus t
- Langkah keempat: menentukan daerah keputusan dengan nilai kritis 4,541. Untuk notasi (<) maka nilai ini otomatis berubah menjadi – 4,541.
- Langkah kelima: mengambil keputusan untuk menolak Ho dan menerima Ho dengan membandingkan nilai alpha dengan nilai uji-t
Baca Juga : Angka Romawi
Dua Sisi
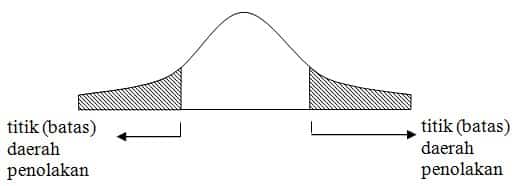
Dua sisi kita gunakan jika dalam perumusan hipotesa digunakan notasi “sama dengan” (=). Gambar distribusinya adalah sebagai berikut:
Contoh
Jika dalam suatu penelitian ditentukan bahwa n = 16 dan nilai alpha 0,05 maka untuk mengetahui nilai titik dalam distribusi yang ditunjukkan dengan tabel t untuk dua sisi adalah sebagai berikut:
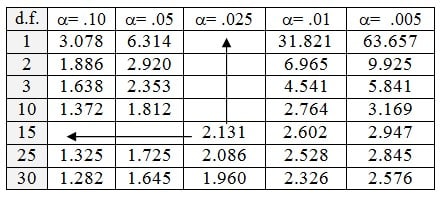
- Langkah pertama: Merumuskan hipotesa untuk uji statistik dua sisi dan menentukan nilai kritis t dua sisi (a/2, v). Untuk uji dua sisi nilai alpha adalah 0,05/2 = 0,025 dan derajat bebas v = n – 1 = 16 – 1 = 15.
- Langkah kedua : Perhatikan tabel distribusi t (dalam BMP lihat halaman 9.22). Sebagaimana mencari nilai kritis t satu sisi, cari nilai alpha pada kolom horizontal paling atas dan derajat bebas (d.f.) pada kolom vertikal paling kiri. Diperoleh nilai kritis t adalah 2,131
- Langkah ketiga: melakukan uji statistik t dengan rumus t
- Langkah ketiga: menentukan daerah keputusan dengan nilai kritis (2,131) uji dua arah
- Langkah keempat: mengambil keputusan untuk menolak Ho dan menerima Ho dengan membandingkan nilai alpha dengan nilai uji-t
Demikianlah Penjelasan artikel diatas tentang Tabel T Statistik – Pengertian, Rumus, Contoh Soal Dan Nilai tentang semoga dapat bermanfaat bagi pembaca setia DosenPendidikan.Com