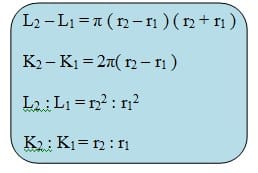Keliling Lingkaran – Pengertian, Rumus, Contoh Soal Dan Materi– DosenPendidikan.Com– Untuk menghitung luas sebuah lingkaran, kita perbandingkan luas lingkaran ini dengan luas segibanyak-segibanyak beraturan yang dilukiskan di dalam dan di luar lingkaran itu. Luas segibanyak luar beraturan senantiasa lebih besar daripada luas lingkaran, sedangkan luas segibanyak dalam beraturan lebih kesil daripada luaslingkaran.
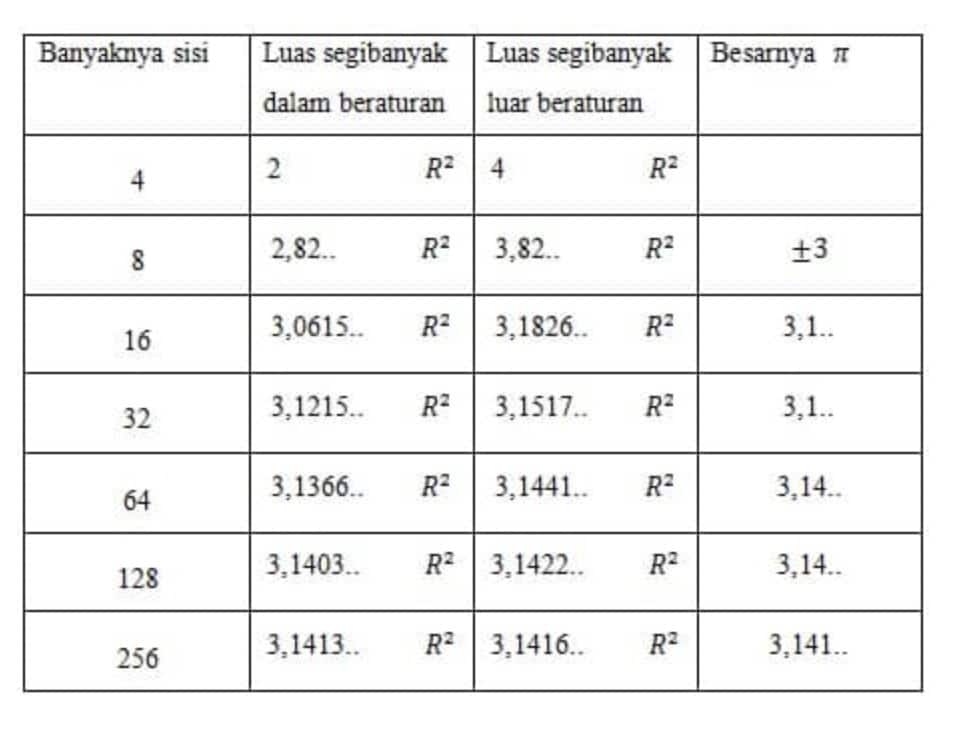
Ini terlihat pada gambar, dari gambat jelas keli segidelapan beraturan lebih mendekati luaas lingkaran dari luas bujur sangkar. Bertambah banyak segibanyak itu, bertambah mendekati luas-luas itu semuanya. Ini juga terbukti dari tabel dibawah ini.
Luas lingkaran biasanya dinyatakan dengan kuadrat jari-jarinya. Bilangan memperkalikan kuadrat jari-jari itu untuk memperoleh luas lingkaran, dinyatakan dengan huruf yunani adalah huruf yunani yang tak terukur. Bilangan dapat diketahui sampai beberapa angka dibelakang koma.
Baca Juga : Rumus Deret Geometri
Jadi lingkaran x setengah jari-jari = luas lingkaran,
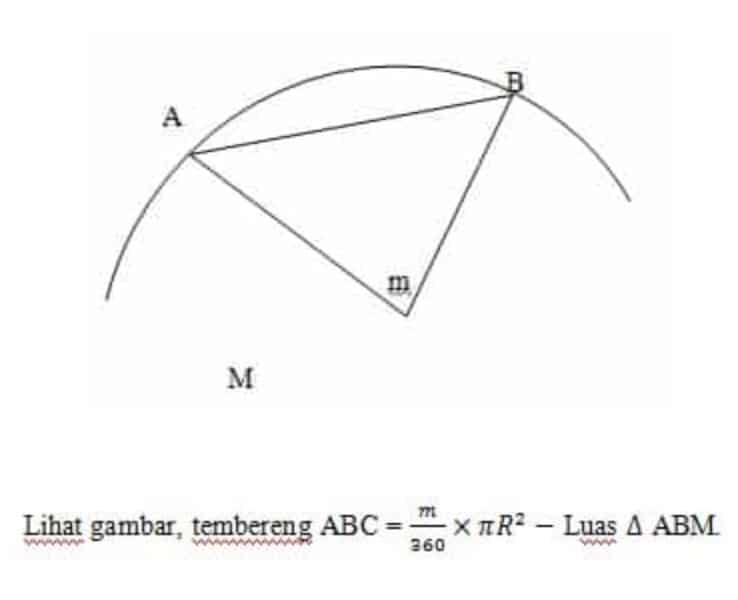
Luas lingkaran dengan pusat O jari-jari r dapat didekati dengan luas dari beberapa segitiga samakaki dengan puncak di O danpanjang masing-masing sisi sama kakinya r. Jika kita mengkonstruksikan segitiga samakaki sebanyak n buah
maka jumlah seluruh luas segitiga akan semakin mendekati luas lingkaran.
Jika terdiri dari n segitiga, maka besar sudut
sehingga luas segitiga tersebut adalah
Jadi luas n segitiga
Baca Juga : Rumus Volume Tabung
Materi Keliling Lingkaran
- Keliling Lingkaran
Coba kamu amati gambar di bawah ini secara seksama.
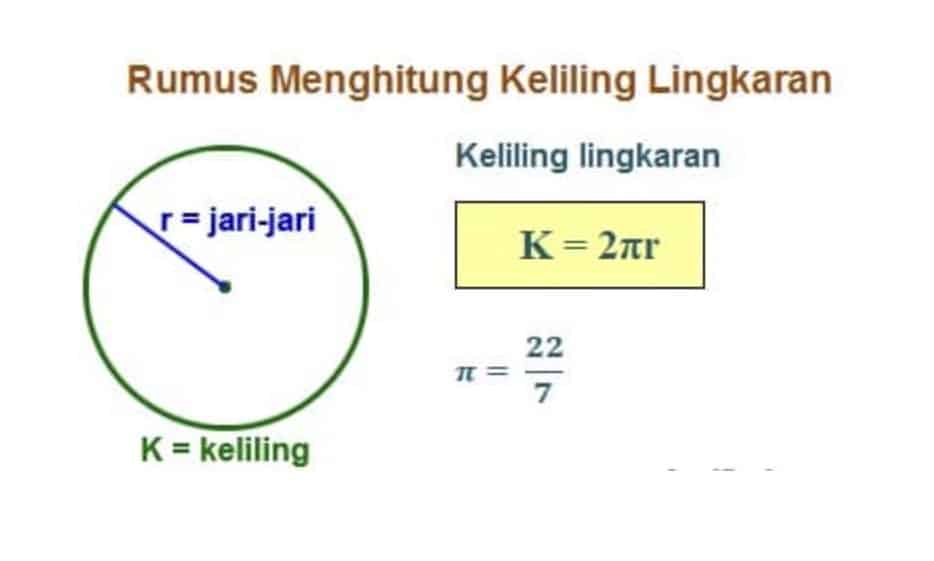
Gambar (a) menunjukkan sebuah lingkaran dengan titik A terletak di sebarang lengkungan lingkaran. Jika lingkaran tersebut dipotong di titik A, kemudian direbahkan, hasilnya adalah sebuah garis lurus AA‘ seperti pada gambar (b). Panjang garis lurus tersebut merupakan keliling lingkaran. Jadi, keliling lingkaran adalah panjang lengkungan pembentuk lingkaran tersebut (Nuharini dan Wahyuni, 2008:140-148).
Bagaimana menghitung keliling lingkaran? Misalkan, diketahui sebuah lingkaran yang terbuat dari kawat. Keliling tersebut dapat dihitung dengan mengukur panjang kawat yang membentuk lingkaran tersebut. Selain dengan cara di atas, keliling sebuah lingkaran dapat juga ditentukan menggunakan rumus. Akan tetapi, rumus ini bergabung pada sebuah nilai, yaitu π (dibaca phi). Berapakah nilai π? Untuk mengetahuinya, lakukan kegiatan berikut :
- Siapkan bahan-bahan seperti kertas, jangka, benang kasur, dan penggaris.
- b. Dengan menggunakan jangka, buatlah lima lingkaran dengan panjang diameter yang berbeda-beda.
- c. Kemudian, hitunglah keliling setiap lingkaran yang telah kamu buat. Caranya dengan mengimpitkan benang kasur pada setiap lingkaran tadi.
- d. Ukurlah panjang benang kasur tadi.
- Catat hasilnya pada tabel berikut.
Jika telah melakukan kegiatan diatas dengan teliti, akan diperoleh nilai yang sama untuk perbandingan keliling dan diameter pada setiap lingkaran. Nilai tersebut adalah 3,141592…. Inilah yang dimaksud dengan nilai π (phi). Jika dibulatkan dengan pendekatan, diperoleh π = 3,14. Oleh
Baca Juga : Rumus Cermin Cembung
Contoh Soal
Sebuah lingkaran memiliki panjang diameter 28 cm. Tentukanlah:
- panjang jari-jari,
- keliling lingkaran.
Jawab:
Diketahui d = 28 cm
- d = 2 . r maka 28 = 2 . r
Jadi, panjang jari-jari lingkaran adalah 14 cm
- K = π . d
Jadi, keliling lingkaran adalah 66 cm
Menghitung Perubahan Luas dan Keliling Lingkaran Jika Jari-Jari Berubah
Misalkan lingkaran berjari-jari r1, diperbesar sehingga jari-jarinya menjadi r2, dengan r2 > r1. Jika luas lingkaran semula adalah L1 dan luas lingkaran setelah mengalami perubahan jari-jari adalah L2 maka selisih kedua lingkaran adalah
L2 – L1 = π r22 – π r12
= π ( r22 – r12 )
= π ( r2 – r1 ) ( r2 + r1 )
Jika keliling lingkaran semula adalah K1 dan keliling setelah mengalami perubahan jari-jari adalah K2 maka selisih keliling kedua lingkaran adalah
K2 – K1 = 2πr2 – 2πr1
= 2π( r2 – r1 )
Kalian juga dapat menghitung perbandingan luas dan keliling lingkaran jika jari-jari berubah.
Perbandingan luas kedua lingkaran sebagai berikut.
L2 : L1 = π r22 : π r12
= r22 : r12
Adapun perbandingan kelilingnya adalah
K2 : K1 = 2πr2 : 2πr1
= r2 : r1
Dari uraian di atas dapat disimpulkan bahwa lingkaran yang berjari-jari r1, setelah mengalami perubahan jari-jari menjadi r2 dengan r2 > r1, maka selisih serta perbandingan luas dan kelilingnya sebagai berikut.
Baca Juga : Lensa Cekung – Pengertian, Sifat, Rumus, Sinar Istimewa dan Contoh
Contoh:
Hitunglah selisih serta perbandingan luas dan keliling lingkaran yang berjari-jari 2 cm dan 4 cm.
Jawab:
Lingkaran berjari-jari 2 cm, maka r1 = 2
Lingkaran berjari-jari 4 cm, maka r2 = 4
Selisih luas = L1 – L2
- = π (r2 – r1) (r2 + r1)
- = π (4 – 2) (4 + 2)
- = 12π cm2
Selisih keliling = K2 – K1
- = 2π (r2 – r1)
- = 2π (4 – 2)
- = 4π cm
Perbandingan luas = L2 : L1
- = r22 : r12
- = 42 : 22
- = 16 : 4
- = 4 : 1
Perbandingan keliling = K2 : K1
- = r2 : r1
- = 4 : 2
- = 2 : 1
Pembuktian Emiris Rumus Luas Lingkaran
Jika jari-jari lingkaran adalah r, maka rumus ukuran luas daerah lingkaran adalah
Untuk membuktikan rumus luas daerah lingkaran dapat dilakukan pembuktian secara empiris. Pembuktian rumus luas daerah lingkaran secara empiris yang lazim dilakukan adalah dengan cara memotong-motong lingkaran sehingga menjadi juring-juring kemudian membentuknya menjadi persegi panjang atau jajargenjang. Sehingga rumus luas daerah lingkaran dapat diturunkan dari rumus luas daerah persegi panjang atau jajargenjang.
- Pembuktian Rumus Luas Lingkaran dengan Menurunkan dari Rumus Luas Persegi Panjang
Lingkaran dipotong-potong menjadi 8 juring, dan salah satu juring dibagi 2 sama menurut jari-jari. Selanjutnya disusun secara zigzag ke samping dengan menempelkan sisi jari-jari dari masing-masing juring sehingga mendekati terbentuk persegi panjang seperti terlihat pada gambar 5.5 dan 5.6 berikut
Jika rumus luas persegi panjang adalah
L = panjang x lebar,
Maka diperoleh rumus luas lingkaran, yaitu
- Pembuktian Rumus Luas Lingkaran dengan Menurunkan dari Rumus Luas Jajargenjang
Lingkaran dipotong-potong menjadi 8 juring.selanjutnya disusun secara zig-zag ke samping dengan menempelkan sisi jari-jari dari masing-masing juring sehingga mendekati terbentuk peersegi panjang seperti terlihat pada gambar 5.7 dan5.8 berikut.
Jika rumus luasjajargenjang adalah
L = alas x tinggi
Maka diperoleh rumus luas lingkaran yaitu
Baca Juga : Volume Bola
- Pembuktian Rumus Luas Lingkaran dengan Menurunkan dari Rumus Luas Segitiga
Untuk membuktikan rumus luas lingkaran dengan menurunkan dari rumus luas segitiga, lingkaran dibagi menjadi juring-juring sebanyak 4,9, 16, 25, 36, ……atau sebanyak , kemudian disusun sedemikian rupa sehingga membentuk segitiga sama kaki. Berikut ini lingkaran yang dipotong menjadi 4 juring (gambar 5.9 dan 5.10) dan menjadi 16 juring (gambar 5.11, 5.12).
Pada gambar 5.11 susunan tersebut nampak jelasbahwa susunan tersebut membentuk segitiga samakaki. Akan tampak sangat jelas jika lingkaran dipotong menjadi 36, 49, 64juring,dan seterusnya.
Perhatikan gambar 5.11. pandang gambar tersebut sebagaisegitiga samakaki.segitiga samakaki tersebut adalah bentukan 16 juring darisebuah lingkaran.
Demikian penjelasan artikel diatas tentang Keliling Lingkaran – Pengertian, Rumus, Contoh Soal Dan Materi semoga bermanfaat bagi semua pembaca DosenPendidikan.Com